题目内容
设x∈R，向量
=（1，2），
=（x，1）
（Ⅰ）当
+2
与2
-
平行时，求x；
（Ⅱ）当
+2
与2
-
垂直时，求|
+
|．
| a |
| b |
（Ⅰ）当
| a |
| b |
| a |
| b |
（Ⅱ）当
| a |
| b |
| a |
| b |
| a |
| b |
考点：平面向量数量积的坐标表示、模、夹角
专题：平面向量及应用
分析：（I）利用向量运算法则和向量共线定理即可得出．
（II）利用向量垂直与数量积的关系、数量积的性质即可得出．
（II）利用向量垂直与数量积的关系、数量积的性质即可得出．
解答：
解：（Ⅰ）∵
+2
=（1，2）+2（x，1）=（1+2x，4），2
-
=2（1，2）-（x，1）=（2-x，3），
又
+2
与2
-
平行，∴4（2-x）-3（1+2x）=0，化为2x=1，解得x=
．
（Ⅱ）∵
⊥
，∴（1+2x）（2-x）+12=0，
化为2x2-3x-14=0，
解得 x=
或x=-2，
当x=-2时，
=(-2，1)，
+
=（-1，3），∴|
+
|=
=
．
当x=
时，
=(
，1)，∴
+
=(
，3)，∴|
+
|=
=
．
∴|
+
|=
或
．
| a |
| b |
| a |
| b |
又
| a |
| b |
| a |
| b |
| 1 |
| 2 |
（Ⅱ）∵
| a |
| b |
化为2x2-3x-14=0，
解得 x=
| 7 |
| 2 |
当x=-2时，
| b |
| a |
| b |
| a |
| b |
| (-1)2+32 |
| 10 |
当x=
| 7 |
| 2 |
| b |
| 7 |
| 2 |
| a |
| b |
| 9 |
| 2 |
| a |
| b |
(
|
3
| ||
| 2 |
∴|
| a |
| b |
| 10 |
3
| ||
| 2 |
点评：本题考查了向量运算法则及其性质、向量共线定理、向量垂直与数量积的关系，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
log39=（ ）
| A、1 | ||
| B、2 | ||
| C、3 | ||
D、
|
曲线y=sinx在x=
处的切线方程是（ ）
| π |
| 2 |
| A、y=0 | B、y=x+1 |
| C、y=x | D、y=1 |
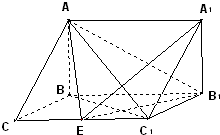在三棱拄ABC-A1B1C1中，AB⊥侧面BB1C1C，已知BC=1，∠BCC1=