题目内容
求证：函数f（x）=
在区间（-∞，-2）上是增函数．
| x |
| x+2 |
考点：函数单调性的判断与证明
专题：导数的综合应用
分析：求f′（x），根据导数符号即可证明该函数的单调性．
解答：
证明：f′（x）=
=
＞0；
∴函数f（x）（-∞，-2）上是增函数．
| x+2-x |
| (x+2)2 |
| 2 |
| (x+2)2 |
∴函数f（x）（-∞，-2）上是增函数．
点评：考查通过对函数求导，根据导数符号证明函数单调性的方法．
练习册系列答案
相关题目
若函数y=ax-ex有小于零的极值点，则实数a的取值范围是（ ）
| A、（0，+∞） |
| B、（0，1） |
| C、（-∞，1） |
| D、（-1，1） |
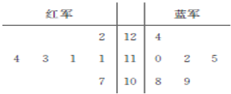解放军某部在实兵演练对抗比赛中，红、蓝两个小组均派6人参加实弹射击，其所得成绩的茎叶图如图所示．