题目内容
已知函数f（x）=
+a的图象经过点（1，2）．
（1）求a的值；
（2）证明函数在（0，+∞）上单调递减；
（3）若函数f（x）在[n，n+1]（n＞0）上的最大值为4，求n的值．
| 1 |
| x |
（1）求a的值；
（2）证明函数在（0，+∞）上单调递减；
（3）若函数f（x）在[n，n+1]（n＞0）上的最大值为4，求n的值．
考点：函数单调性的性质,函数单调性的判断与证明,函数的值
专题：函数的性质及应用
分析：（1）代值计算即可．
（2）利用导数判断即可，先求导，再判断单调性，
（3）根据单调性，知当x=n时，函数有最大值，代值计算即可
（2）利用导数判断即可，先求导，再判断单调性，
（3）根据单调性，知当x=n时，函数有最大值，代值计算即可
解答：
解：（1）f（x）=
+a的图象经过点（1，2）．
∴f（1）=1+a=2，
解得a=1，
（2）∵f′（x）=-
＜0，
∴函数f（x）在（0，+∞）上单调递减；
（3）∵函数f（x）在（0，+∞）上单调递减；
∴当x=n时，函数有最大值，
∴
+1=4，
解得n=
．
| 1 |
| x |
∴f（1）=1+a=2，
解得a=1，
（2）∵f′（x）=-
| 1 |
| x2 |
∴函数f（x）在（0，+∞）上单调递减；
（3）∵函数f（x）在（0，+∞）上单调递减；
∴当x=n时，函数有最大值，
∴
| 1 |
| n |
解得n=
| 1 |
| 3 |
点评：本题主要考查了导数与函数的单调性及最值的问题，属于基础题．
练习册系列答案
相关题目
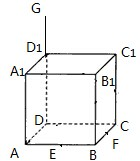如图，G是正方体ABCD-A1B1C1D1的棱的DD1延长线上的一点，E、F是棱AB、BC的中点，试分别画出：
莆田往福州的某次动车途中经停福清站，为了方便莆田市VIP客户搭乘，车站信息管理员对该次动车VIP车厢（共4个座位）莆田至福州的全程空座位数n进行统计，得到10个车次样本数据的茎叶图，如图所示．（全程空座位数即莆田至福清、福清至福州两个站段的空座位数之和）