Question

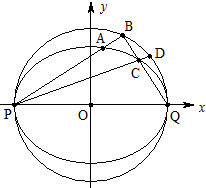已知椭圆C₁：

x2

a2

+

y2

b2

=1（a＞b＞0）和圆C₂：x²+y²=r²都过点P（-1，0），且椭圆C₁的离心率为

2

2

，过点P作斜率为k₁，k₂的直线分别交椭圆C₁，圆C₂于点A，B，C，D（如图），k₁=λk₂，若直线BC恒过定点Q（1，0），则λ=

 

．

Answer 1

考点：直线与圆锥曲线的关系

专题：直线与圆,圆锥曲线的定义、性质与方程

分析：根据k₁=λk₂，应该找到k₁，k₂的关系式，再结合直线分别与直线相交，交点为A，B，C，D，用k把相应的点的坐标表示出来（将直线代入椭圆的方程消去关于x的一元二次方程，借助于韦达定理将A，B，C，D表示出来），再想办法把Q点坐标表示出来，再利用B，C，Q三点共线构造出关于k₁，k₂的方程，化简即可．

解答： 解：C1：x2+2y2=1；C2：x2+y2=1
设A（x_A，y_A）、B（x_B，y_B）、C（x_C，y_C）、D（x_D，y_D），
由

x2+2y2=1 y=k1(x+1)

得：(1+2

k

2 1

)x2+4

k

2 1

x+2

k

2 1

-1=0，
∵x_P=-1，∴xA=

1-2 k 2 1

1+2 k 2 1

，则点A的坐标为：A(-1+

2

1+2 k 2 1

，

2k1

1+2 k 2 1

)
由

x2+y2=1 y=k1(x+1)

得：(1+

k

2 1

)x2+2

k

2 1

x+

k

2 1

-1=0，
∵x_P=-1，∴xB=

1- k 2 1

1+ k 2 1

，则点B的坐标为：B(-1+

2

1+ k 2 1

，

2k1

1+ k 2 1

)
同理可得：C(-1+

2

1+2 k 2 2

，

2k2

1+2 k 2 2

)，D(-1+

2

1+ k 2 2

，

2k2

1+ k 2 2

)，
根据B、C、Q三点共线，

BC

=λ

CQ

，结合Q（1，0）
所以(

2

1+2k22

-

2

1+2k12

，

2k2

1+k22

-

2k1

1+k12

)=λ（2-

2

1+2k22

，-

2k2

1+2k22

）
化简得λ=2
故答案为：2．

点评：本题的计算量较大，关键是如何找到k₁，k₂间的关系表示出来，最终得到λ的值．