题目内容
函数y=
的定义域为 ．
| ||
| 3x2+5x-2 |
考点：函数的定义域及其求法
专题：函数的性质及应用
分析：根据函数成立的条件，即可求出结论．
解答：
解：要是函数有意义，则
，
则
即x≥-1且x≠
，
故函数的定义域为[-1，
）∪（
，+∞），
故答案为：[-1，
）∪（
，+∞）
|
则
|
即x≥-1且x≠
| 1 |
| 3 |
故函数的定义域为[-1，
| 1 |
| 3 |
| 1 |
| 3 |
故答案为：[-1，
| 1 |
| 3 |
| 1 |
| 3 |
点评：本题主要考查函数定义域的求解，要求熟练掌握常见函数成立的条件．
练习册系列答案
名师金手指领衔课时系列答案
相关题目
“k=±
”是“直线x-y+k=0与圆x2+y2=1相切”的（ ）
| 2 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也也必要条件 |
下列各组两个集合P和Q，表示同一集合的是（ ）
A、P={1，
| ||
| B、P={π}，Q={3.14159} | ||
| C、P={2，3}，Q={3，2} | ||
| D、P={1，2}，Q={（1，2）} |
已知向量
=（2，1），
=（1，x），若
-
与
+4
平行，则实数x等于（ ）
| a |
| b |
| a |
| b |
| a |
| b |
A、
| ||
B、
| ||
| C、-1 | ||
| D、1 |
下列各式的值是负值的是（ ）
| A、cos（-31°） |
| B、sin 13° |
| C、tan 242° |
| D、cos 114° |
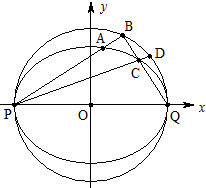已知椭圆C1：