题目内容
求函数y=
的最值．
| 2-sinα |
| 2+cosα |
考点：函数的最值及其几何意义
专题：函数的性质及应用
分析：原式可化为sin（α+∅）=
，利用三角函数的有界性即可求得结论．
| 2-2y | ||
|
解答：
解：y=
，即sina+ycosa=2-2y，
sin（α+∅）=2-2y，
sin（α+∅）=
，
∵|sin（a+∅）|≤1
∴|
|≤1，
解得：
≤y≤
．
| 2-sinα |
| 2+cosα |
| 1+y2 |
sin（α+∅）=
| 2-2y | ||
|
∵|sin（a+∅）|≤1
∴|
| 2-2y | ||
|
解得：
4-
| ||
| 3 |
4+
| ||
| 3 |
点评：本题考查函数值域的求法，利用函数的有界性求函数的值域，属于中档题．
练习册系列答案
天天向上课时同步训练系列答案
阳光课堂同步练习系列答案
相关题目
下列各式的值是负值的是（ ）
| A、cos（-31°） |
| B、sin 13° |
| C、tan 242° |
| D、cos 114° |
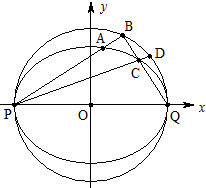已知椭圆C1：