Question

19．如图，三棱柱ABC-A₁B₁C₁中，A₁B⊥平面ABC，且AB⊥AC．
（1）求证：AC⊥BB₁；
（2）若AB=AC=A₁B=2，M为B₁C₁的中点，求二面角M-AB-A₁平面角的余弦值．

Answer 1

分析 （1）推导出A₁B⊥AC，AB⊥AC，从而AC⊥平面A₁ABB₁，由此能证明AC⊥BB₁．
（2）过点A作AY∥A₁B，以射线AB，AC，AY为x，y，z正半轴建立空间直角坐标系，利用向量法能求出二面角M-AB-A₁平面角的余弦值．

解答 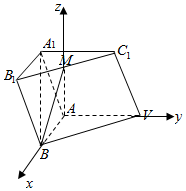证明：（1）∵三棱柱ABC-A₁B₁C₁中，A₁B⊥平面ABC，
∴A₁B⊥AC，∵AB⊥AC，A₁B∩AB=B，
∴AC⊥平面A₁ABB₁，
∵BB₁?平面A₁ABB₁，∴AC⊥BB₁．
解：（2）过点A作AY∥A₁B，
∵A₁B⊥平面ABC，∴AY⊥平面ABC，
又AB⊥AC，以射线AB，AC，AY为x，y，z正半轴建立空间直角坐标系，
由AB=AC=A₁B=2，得A（0，0，0），B（2，0，0），C（0，2，0），A₁（2，0，2），
由$\overrightarrow{B{B_1}}=\overrightarrow{C{C_1}}=（2，0，2）$，得B₁（4，0，2），C₁（2，2，2），M为B₁C₁的中点，
M（3，1，2），$\overrightarrow{AM}=（3，1，2），\overrightarrow{AB}=（2，0，0）$，
设平在ABM的法向量$\overrightarrow{m}$=（x，y，z），
则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{AM}=3x+y+2z=0}\\{\overrightarrow{m}•\overrightarrow{AB}=2x=0}\end{array}\right.$，取y=2，得平面ABM的法向量$\overrightarrow m=（0，2，-1）$，
$\overrightarrow{A{A_1}}=（2，0，2），\overrightarrow{AB}=（2，0，0）$，平面ABA₁的法向量$\overrightarrow n=（0，1，0）$，
∴$cos\left?{\overrightarrow m，\overrightarrow n}\right＞=\frac{\overrightarrow m•\overrightarrow n}{{|{\overrightarrow m}|•|{\overrightarrow n}|}}=\frac{2}{{1•\sqrt{5}}}=\frac{{2\sqrt{5}}}{5}$，
设二面角M-AB-A₁的平面角为θ，由图知θ锐角，
∴二面角M-AB-A₁平面角的余弦值为$cosθ=\frac{{2\sqrt{5}}}{5}$．

点评 本题考查线线垂直的证明，考查二面角的余弦值的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查推理论证能力、运算求解能力、空间想象能力，考查化归与转化思想，是中档题．