题目内容
已知椭圆C:
+
=1(a>b>0)的离心率为
,右焦点到直线l:x-y+4=0的距离为
.
(Ⅰ)求椭圆C的方程;
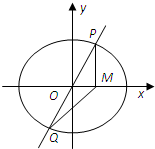
(Ⅱ)过直线l上的动点P作椭圆C的切线PM、PN,切点分别为M、N,连结MN.
(1)证明:直线MN恒过定点Q;
(2)证明:当MN∥l时,定点Q平分线段MN.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
5
| ||
| 2 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)过直线l上的动点P作椭圆C的切线PM、PN,切点分别为M、N,连结MN.
(1)证明:直线MN恒过定点Q;
(2)证明:当MN∥l时,定点Q平分线段MN.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)由已知条件推导出
=
,
=
,由此能求出椭圆方程.
(Ⅱ)(1)设P(x0,y0).M(x1,y1).N(x2,y2),由已知条件推导出
+y0y=1是直线MN的方程,其中(x0,y0)满足直线l的方程,由此能求出直线MN恒过定点Q(-
,
).
(2)由(1)知当MN∥l时,MN的方程为x-y+
=0,与椭圆方程联立,得x2+x-
=0,由此能证明点Q平分线段MN.
| c |
| a |
| ||
| 2 |
| c+4 | ||
|
5
| ||
| 2 |
(Ⅱ)(1)设P(x0,y0).M(x1,y1).N(x2,y2),由已知条件推导出
| x0x |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
(2)由(1)知当MN∥l时,MN的方程为x-y+
| 3 |
| 4 |
| 7 |
| 24 |
解答:
解:(Ⅰ)∵椭圆C:
+
=1(a>b>0)的离心率为
,
右焦点到直线l:x-y+4=0的距离为
.
∴
=
,
=
,
解得c=1,a=
,b=1,
∴所求椭圆方程为
+y2=1.…(3分)
(Ⅱ)(1)证明:设P(x0,y0).M(x1,y1).N(x2,y2).
则椭圆过点M、N的切线方程分别为
+y1y=1,
+y2y=1.…(5分)
∵两切线都过点P,则有
+y1y0=1,
+y2y0=1.
这表明M.N均在直线
+y0y=1①上.
由两点决定一条直线知,
式①就是直线MN的方程,其中(x0,y0)满足直线l的方程.…(7分)
当点P在直线l上运动时,
可理解为x0取遍一切实数,相应的y0为y0=x0+4.
代入①消去y0得
x+(x0+4)y-1=0
变形可得x0(
+y)+(4y-1)=0对一切x0∈R恒成立.
∴
由此解得直线MN恒过定点Q(-
,
).…(10分)
(2)证明:由(1)知当MN∥l时,MN的方程为x-y+
=0
将此方程与椭圆方程联立,消去y得x2+x-
=0.…(11分)
设MN截椭圆所得弦的中点为Q′(x′,y′),
x′=
=-
,y′=x′+
=
,∴点Q′与Q重合.
所以点Q平分线段MN.…(13分)
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
右焦点到直线l:x-y+4=0的距离为
5
| ||
| 2 |
∴
| c |
| a |
| ||
| 2 |
| c+4 | ||
|
5
| ||
| 2 |
解得c=1,a=
| 2 |
∴所求椭圆方程为
| x2 |
| 2 |
(Ⅱ)(1)证明:设P(x0,y0).M(x1,y1).N(x2,y2).
则椭圆过点M、N的切线方程分别为
| x1x |
| 2 |
| x2x |
| 2 |
∵两切线都过点P,则有
| x1x0 |
| 2 |
| x2x0 |
| 2 |
这表明M.N均在直线
| x0x |
| 2 |
由两点决定一条直线知,
式①就是直线MN的方程,其中(x0,y0)满足直线l的方程.…(7分)
当点P在直线l上运动时,
可理解为x0取遍一切实数,相应的y0为y0=x0+4.
代入①消去y0得
| x0 |
| 2 |
变形可得x0(
| x |
| 2 |
∴
|
由此解得直线MN恒过定点Q(-
| 1 |
| 2 |
| 1 |
| 4 |
(2)证明:由(1)知当MN∥l时,MN的方程为x-y+
| 3 |
| 4 |
将此方程与椭圆方程联立,消去y得x2+x-
| 7 |
| 24 |
设MN截椭圆所得弦的中点为Q′(x′,y′),
x′=
| x1+x2 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
| 1 |
| 4 |
所以点Q平分线段MN.…(13分)
点评:本题考查椭圆方程的求法,考查直线恒过定点的证明,考查定点平分线段的证明,解题时要认真审题,注意中点坐标公式的合理运用.

练习册系列答案
相关题目
 已知椭圆C的两焦点F1(-1,0)、F2(1,0),离心率为
已知椭圆C的两焦点F1(-1,0)、F2(1,0),离心率为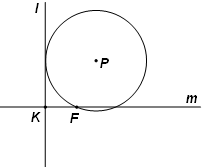 如图,已知定点F及定直线l,直线m经过F与l垂直,垂足为K,|FK|=p(p>0),动圆P经过F与l相切.
如图,已知定点F及定直线l,直线m经过F与l垂直,垂足为K,|FK|=p(p>0),动圆P经过F与l相切.