题目内容
已知函数f(x)的定义域为[0,+∞),值域是[0,+∞)的子集,且满足下列条件:
①对任意x,y∈[0,+∞),都有f[xf(y)]•f(y)=f(x+y);
②f(2)=0;
③f(x)≠0(0≤x<2).
(1)当x≥2时,求证:f(x)=0;
(2)求f(x)的解析式.
①对任意x,y∈[0,+∞),都有f[xf(y)]•f(y)=f(x+y);
②f(2)=0;
③f(x)≠0(0≤x<2).
(1)当x≥2时,求证:f(x)=0;
(2)求f(x)的解析式.
考点:抽象函数及其应用,函数的定义域及其求法,函数的值域,函数解析式的求解及常用方法
专题:综合题,函数的性质及应用
分析:(1)令y=2,代入①,根据②即可证明;
(2)令x=y=0,由①结合③,可得f(0)=1,令2=(2-x)+x,代入①,结合③得到f[xf(2-x)]=0,
由②得xf(2-x)=2,从而得到f(x)=
,也适合x=0,故可得f(x)的解析式.
(2)令x=y=0,由①结合③,可得f(0)=1,令2=(2-x)+x,代入①,结合③得到f[xf(2-x)]=0,
由②得xf(2-x)=2,从而得到f(x)=
| 2 |
| 2-x |
解答:
(1)证明:令y=2,则由①得,f[xf(2)]•f(2)=f(x+2),
再由②得,f(x+2)=0,
∵x≥0,∴当x≥2时,f(x)=0;
(2)解:由(1)得,当x≥2时,f(x)=0;
当x=y=0时,f(0f(0))•f(0)=f(0),则f(0)=0或1,
由③f(0)≠0,故f(0)=1,
令0<x<2,则0<2-x<2,
由①得,f(2)=f[(2-x)+x}=f[xf(2-x)]•f(2-x)=0,
由③得,f(2-x)≠0,故f[xf(2-x)]=0,
由f(2)=0,则xf(2-x)=2,即f(2-x)=
,
∴f(x)=
,也适合x=0,
∴f(x)=
.
再由②得,f(x+2)=0,
∵x≥0,∴当x≥2时,f(x)=0;
(2)解:由(1)得,当x≥2时,f(x)=0;
当x=y=0时,f(0f(0))•f(0)=f(0),则f(0)=0或1,
由③f(0)≠0,故f(0)=1,
令0<x<2,则0<2-x<2,
由①得,f(2)=f[(2-x)+x}=f[xf(2-x)]•f(2-x)=0,
由③得,f(2-x)≠0,故f[xf(2-x)]=0,
由f(2)=0,则xf(2-x)=2,即f(2-x)=
| 2 |
| x |
∴f(x)=
| 2 |
| 2-x |
∴f(x)=
|
点评:本题主要考查抽象函数及应用,考查解决的常用方法:赋值法,正确赋值(式)是解题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 已知椭圆C的两焦点F1(-1,0)、F2(1,0),离心率为
已知椭圆C的两焦点F1(-1,0)、F2(1,0),离心率为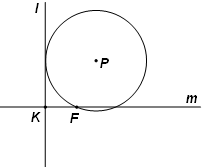 如图,已知定点F及定直线l,直线m经过F与l垂直,垂足为K,|FK|=p(p>0),动圆P经过F与l相切.
如图,已知定点F及定直线l,直线m经过F与l垂直,垂足为K,|FK|=p(p>0),动圆P经过F与l相切.