题目内容
已知抛物线C:x2=ay(a>0),M为直线l:y=-1上任意一点,过点M作抛物线C的两条切线MA,MB,切点分别为A,B.
(Ⅰ)当a=4且M的坐标为(0,-1)时,求过M,A,B三点的圆的方程;
(Ⅱ)证明:直线AB恒过定点;
(Ⅲ)是否存在抛物线C,使得以A、B为直径的圆恒过点M,若有,求出这样的抛物线,若没有,说明理由.
(Ⅰ)当a=4且M的坐标为(0,-1)时,求过M,A,B三点的圆的方程;
(Ⅱ)证明:直线AB恒过定点;
(Ⅲ)是否存在抛物线C,使得以A、B为直径的圆恒过点M,若有,求出这样的抛物线,若没有,说明理由.
考点:直线与圆锥曲线的关系,圆的标准方程
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)当M的坐标为(0,-1)时,设过M点的切线方程为y=kx-1,由
,消y得x2-4kx+4=0,由此利用根的判别式、圆的性质,结合已知条件能求出过M,A,B三点的圆的方程.
(Ⅱ)设M(x0,0),A(x1,
x12),B(x2,
x22),由y=
x2,利用导数的几何意义推导出AB的方程为y=
x+1,由此能证明直线AB过定点(0,1).
(Ⅲ)假设这样的点存在,则
•
=0恒成立,从则(x1-x0,
x12+1)(x2-x0,
x22+1)=0恒成立,由此推导出这样的抛物线存在,其方程为x2=4y.
|
(Ⅱ)设M(x0,0),A(x1,
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 2x0 |
| a |
(Ⅲ)假设这样的点存在,则
| MA |
| MB |
| 1 |
| a |
| 1 |
| a |
解答:
(Ⅰ)解:当M的坐标为(0,-1)时,
设过M点的切线方程为y=kx-1,
由
,消y得x2-4kx+4=0,(1)
令△=(4k)2-4×4=0,解得:k=±1,
代入方程(1),解得A(2,1),B(-2,1),
设圆心P的坐标为(0,a),由|PM|=|PB|,得a+1=2,解得a=1,
故过M,A,B三点的圆的方程为x2+(y-1)2=4.…(4分)
(Ⅱ)证明:设M(x0,0),A(x1,
x12),B(x2,
x22),
∵y=
x2,∴y′=
x,
∴直线MA,MB的方程为y=
x1x-
x12,y=
x2x-
x22,…(6分)
∵直线MA,MB过M点,∴-1=
x1x0-
x12,-1=
x2x0-
x22.
∴x1,x2满足方程
x2-
x-1=0,…(8分)
∴x1+x2=2x0,x1x2=-a,
∴AB的方程为y=
x+1,
∴直线AB过定点(0,1).…(10分)
(Ⅲ)解:假设这样的点存在,则
•
=0恒成立
∴(x1-x0,
x12+1)(x2-x0,
x22+1)=0恒成立,…(12分)
∴(
-1)x0+4-a=0对任意的x0恒成立,
∴a=4,这样的抛物线存在,其方程为x2=4y.…(14分)
设过M点的切线方程为y=kx-1,
由
|
令△=(4k)2-4×4=0,解得:k=±1,
代入方程(1),解得A(2,1),B(-2,1),
设圆心P的坐标为(0,a),由|PM|=|PB|,得a+1=2,解得a=1,
故过M,A,B三点的圆的方程为x2+(y-1)2=4.…(4分)
(Ⅱ)证明:设M(x0,0),A(x1,
| 1 |
| a |
| 1 |
| a |
∵y=
| 1 |
| a |
| 2 |
| a |
∴直线MA,MB的方程为y=
| 2 |
| a |
| 1 |
| a |
| 2 |
| a |
| 1 |
| a |
∵直线MA,MB过M点,∴-1=
| 2 |
| a |
| 1 |
| a |
| 2 |
| a |
| 1 |
| a |
∴x1,x2满足方程
| 1 |
| a |
| 2x0 |
| a |
∴x1+x2=2x0,x1x2=-a,
∴AB的方程为y=
| 2x0 |
| a |
∴直线AB过定点(0,1).…(10分)
(Ⅲ)解:假设这样的点存在,则
| MA |
| MB |
∴(x1-x0,
| 1 |
| a |
| 1 |
| a |
∴(
| 4 |
| a |
∴a=4,这样的抛物线存在,其方程为x2=4y.…(14分)
点评:本题考查过M,A,B三点的圆的方程的求法,考查直线AB恒过定点的证明,考查是否存在抛物线C,使得以A、B为直径的圆恒过点M的判断与求法,解题时要注意椭圆、圆、向量、导数等知识点的综合运用.

练习册系列答案
相关题目
在锐角三角形ABC中,角A,B,C对应的边长分别为a,b,c,若a,b,c成等比数列,则cosB的取值范围是( )
A、(0,
| ||||||
B、(0,
| ||||||
C、[
| ||||||
D、[
|
已知函数若f(x)=cosx-log
x,则f(x)在其定义域上零点的个数为( )
| 1 |
| 10 |
| A、1个 | B、3个 | C、5个 | D、7个 |
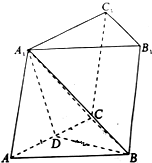 如图,在三棱锥ABC-A1B1C1中,△ABC为等边三角形,AB=2,AA1=
如图,在三棱锥ABC-A1B1C1中,△ABC为等边三角形,AB=2,AA1=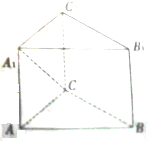 大小已知三棱柱ABC-A1B1C1在某个直角坐标系中,
大小已知三棱柱ABC-A1B1C1在某个直角坐标系中,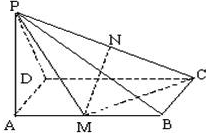 如图所示,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,M、N分别是AB、PC的中点,PA=AD=a.
如图所示,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,M、N分别是AB、PC的中点,PA=AD=a.