Question

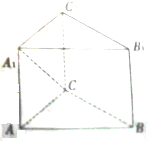大小已知三棱柱ABC-A₁B₁C₁在某个直角坐标系中，

AB

=（

m

2

，

- 3

2

m，0），

AC

=（m，0，0），

AA1

=（0，0，n），m、n＞0，m=

2

n，求直线CA₁与平面A₁ABB₁所成角的大小．

Answer 1

考点：直线与平面所成的角

专题：空间角,空间向量及应用

分析：首先利用线面的垂直求出平面的法向量，进一步利用向量的数量积求出线面的夹角．

解答： 解：根据题意：

A1C

=

AC

-

AA1

=（m，0，0）-（0，0，n）=（m，0，-n）
设平面平面A₁ABB₁的法向量为：

n

=(x，y，z)
则：

AA1 • n =0 AB • n =0

已知

AB

=(

m

2

，

- 3

2

m，0)，

AA1

=(0，0，n)，且m=

2

n
则：

n

=(

3

，1，0)
cos＜

A1C

，

n

＞=

A1C • n

| A1C || n |

=

2

2

＜

A1C

，

n

＞=

π

4

所以：直线CA₁与平面A₁ABB₁所成角的大小

π

4

．

点评：本题考查的知识要点：向量的数量积，向量的加减运算，线面的夹角，法向量的应用．属于基础题型．