题目内容
已知分段函数f（x）=|x-3|+|x+3|，求该函数的单调性和单调区间．
考点：分段函数的应用
专题：计算题,数形结合,函数的性质及应用
分析：分x≤-3，-3＜x＜3，x≥3三段写出函数f（x）的解析式，根据解析式作出函数图象，再由图象得出函数的单调性及单调区间．
解答：
解：当 x≤-3时，f（x）=-（x-3）-（x+3）=-2x，
当-3＜x＜3时，f（x）=-（x-3）+（x+3）=6，
当x≥3时，f（x）=（x-3）+（x+3）=2x．
综上函数的解析式为f（x）=
．
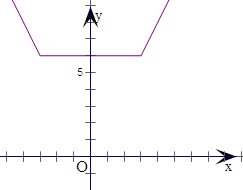
函数的图象如右所示．
由函数f（x）的图象可知函数的递减区间为（-∞，-3]，
函数的递增区间为[3，+∞）．
解：当 x≤-3时，f（x）=-（x-3）-（x+3）=-2x，当-3＜x＜3时，f（x）=-（x-3）+（x+3）=6，
当x≥3时，f（x）=（x-3）+（x+3）=2x．
综上函数的解析式为f（x）=
|
函数的图象如右所示．
由函数f（x）的图象可知函数的递减区间为（-∞，-3]，
函数的递增区间为[3，+∞）．
点评：本题主要考查了分段函数的解析式及图象、函数的单调性及单调区间．培养了学生分类讨论及数形结合的思想方法及解题能力．
练习册系列答案
名校课堂系列答案
相关题目
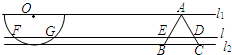如图，半径为1的半圆O与等边△ABC夹在两平行线l1、l2之间．l∥l1，l与半圆相交于F、G两点，与三角形ABC两边相交于E、D两点，设弧
代数式a-5的值为正数时，a应满足条件（ ）
| A、a＜5 | B、a＜4 |
| C、a＞5 | D、a＜0 |