Question

14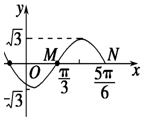．如图为函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜π）图象的一部分．
（1）当x∈[-$\frac{π}{12}$，$\frac{π}{2}$]时，求函数f（x）的值域；
（2）若将函数y=f（x）图象向左平移$\frac{π}{6}$的单位后，得到函数y=g（x）的图象，若g（x）≥$\frac{\sqrt{3}}{2}$，求x的取值范围．

Answer 1

分析 （1）由函数的图象的顶点坐标求出A，由周期求出ω，由五点法作图求出φ的值，可得函数的解析式．
（2）利用函数y=Asin（ωx+φ）的图象变换规律，求得g（x）的解析式，再利用正弦函数的图象和性质，求得g（x）≥$\frac{\sqrt{3}}{2}$的解集．

解答 解：（1）根据函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜π）图象，可得A=$\sqrt{3}$，
$\frac{T}{2}$=$\frac{1}{2}•\frac{2π}{ω}$=$\frac{5π}{6}$-$\frac{π}{3}$，∴ω=2，再根据五点法作图可得2•$\frac{π}{3}$+φ=0，∴φ=-2•$\frac{π}{3}$，
函数f（x）=$\sqrt{3}$sin（2x-$\frac{2π}{3}$）．
当x∈[-$\frac{π}{12}$，$\frac{π}{2}$]时，2x-$\frac{2π}{3}$∈[-$\frac{5π}{6}$，$\frac{π}{3}$]，sin（2x+$\frac{π}{3}$）∈[-1，$\frac{\sqrt{3}}{2}$]，
∴f（x）∈[-$\sqrt{3}$，$\frac{3}{2}$]．
（2）将函数y=f（x）图象向左平移$\frac{π}{6}$的单位后，得到函数y=g（x）=$\sqrt{3}$sin（2x+$\frac{π}{3}$-$\frac{2π}{3}$）
=$\sqrt{3}$sin（2x-$\frac{π}{3}$）的图象，
若g（x）≥$\frac{\sqrt{3}}{2}$，则sin（2x-$\frac{π}{3}$）≥$\frac{1}{2}$，∴2kπ+$\frac{π}{6}$≤2x-$\frac{π}{3}$≤2kπ+$\frac{5π}{6}$，∴kπ+$\frac{π}{4}$≤x≤kπ+$\frac{7π}{12}$，k∈Z，
即要求的x的取值范围为 （kπ+$\frac{π}{4}$，kπ+$\frac{7π}{12}$  ），k∈Z．

点评 本题主要考查由函数y=Asin（ωx+φ）的部分图象求解析式，由函数的图象的顶点坐标求出A，由周期求出ω，由五点法作图求出φ的值；函数y=Asin（ωx+φ）的图象变换规律，正弦函数的图象和性质，属于中档题．