题目内容
9.若$sin(\frac{π}{3}+α)=\frac{1}{3}$,则$cos(α-\frac{7π}{6})$=$-\frac{1}{3}$.分析 利用诱导公式即可求得答案.
解答 解:$cos(α-\frac{7π}{6})$=cos[-π+(α-$\frac{π}{6}$)]=-cos(α-$\frac{π}{6}$)=-sin[$\frac{π}{2}$+(α-$\frac{π}{6}$)]=-sin(α+$\frac{π}{3}$)=$-\frac{1}{3}$,
∴$cos(α-\frac{7π}{6})$=$-\frac{1}{3}$,
故答案为:$-\frac{1}{3}$.
点评 本题考查诱导公式的应用,考查计算能力,转化思想,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.(x-$\frac{1}{2x}$)8的展开式中常数为( )
| A. | $\frac{1}{2}$ | B. | $\frac{35}{8}$ | C. | $\frac{3}{2}$ | D. | -$\frac{3}{2}$ |
1.若三条线段的长度分别为4、6、8,则用这三条线段( )
| A. | 能组成钝角三角形 | B. | 能组成锐角三角形 | ||
| C. | 能组成直角三角形 | D. | 不能组成三角形 |
19.在正项等比数列{an}中,a1009=$\frac{1}{10}$,则lga1+lga2+…+lga2017=( )
| A. | 2015 | B. | -2017 | C. | -2015 | D. | -2016 |
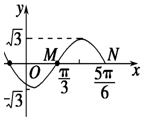 如图为函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)图象的一部分.
如图为函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)图象的一部分. 如图1,在边长为3的正三角形ABC中,E,F,P分别为AB,AC,BC上的点,且满足AE=FC=CP=1.将△
如图1,在边长为3的正三角形ABC中,E,F,P分别为AB,AC,BC上的点,且满足AE=FC=CP=1.将△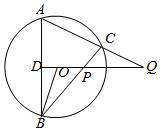 如图,A,B,C是圆O上不共线的三点,OD⊥AB于D,BC和AC分别交DO的延长线于P和Q,求证:∠OBP=∠CQP.
如图,A,B,C是圆O上不共线的三点,OD⊥AB于D,BC和AC分别交DO的延长线于P和Q,求证:∠OBP=∠CQP.