计算:sin187°cos52°+cos7°sin52°=$\frac{\sqrt{2}}{2}$．题目和参考答案——青夏教育精英家教网—

题目内容

19．计算：sin187°cos52°+cos7°sin52°=$\frac{\sqrt{2}}{2}$．

分析利用诱导公式和和与差的公式直接求解即可．

解答解：sin187°cos52°+cos7°sin52°=sin（180°+7°）cos52°+cos7°sin52°=sin52°cos7°-cos52°sin7°=sin（52°-7°）=sin45°=$\frac{\sqrt{2}}{2}$．
故答案为$\frac{\sqrt{2}}{2}$．

点评本题考查了诱导公式的化解能力和和与差的公式计算．属于基础题．

练习册系列答案

10．四名学生报名参加五项体育比赛．每人限报一项，不同的报名方法有种（　　）

4⁵

5⁴

7．已知点P是以F₁，F₂为焦点的椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞0，b＞0}）$上一点，若$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}=0，tan∠P{F_1}{F_2}=\frac{1}{3}$，则椭圆的离心率是（　　）

A．

$\frac{{\sqrt{6}}}{4}$

B．

$\frac{{\sqrt{2}}}{2}$

C．

$\frac{{\sqrt{10}}}{4}$

D．

$\frac{{\sqrt{3}}}{2}$

14．

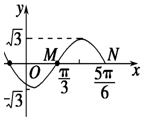如图为函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜π）图象的一部分．
（1）当x∈[-$\frac{π}{12}$，$\frac{π}{2}$]时，求函数f（x）的值域；
（2）若将函数y=f（x）图象向左平移$\frac{π}{6}$的单位后，得到函数y=g（x）的图象，若g（x）≥$\frac{\sqrt{3}}{2}$，求x的取值范围．

4．已知各项都不相等的等差数列{a_n}，满足a_2n=2a_n-3，且a${\;}_{6}^{2}$=a₁•a₂₁，{a_n}的前n项和是S_n，则数列{$\frac{{S}_{n}}{{2}^{n-1}}$}项中的最大值为6．

11．圆ρ=4cos θ的圆心到直线tan（$θ+\frac{π}{2}$）=1的距离为$\sqrt{2}$．

8．（1）从1，2，3，4四个数字中任取两个数字组成两位数，共有多少个不同的两位数？
（2）由1，2，3，4四个数字共能组成多少个没有重复数字的四位数？

14．（x-$\frac{1}{2x}$）⁸的展开式中常数为（　　）

试题分类