题目内容
已知命题A：1≤m≤3，命题B：2＜m＜4，若A，B中有且只有一个真命题，求实数m的取值范围．
考点：命题的真假判断与应用
专题：简易逻辑
分析：根据题意，当A是真命题，B是假命题时，求出m的取值范围；当A是假命题，B是真命题时，求出m的取值范围；再求它们的并集即可．
解答：
解：∵命题A：1≤m≤3，命题B：2＜m＜4，
若A是真命题，B是假命题时，
有
，
解得1≤m≤2；
若A是假命题，B是真命题时，
有
，
解得3＜m＜4；
综上，m的取值范围是{m|1≤m≤2，或3＜m＜4}．
若A是真命题，B是假命题时，
有
|
解得1≤m≤2；
若A是假命题，B是真命题时，
有
|
解得3＜m＜4；
综上，m的取值范围是{m|1≤m≤2，或3＜m＜4}．
点评：本题通过命题真假的判定，考查了简易逻辑的应用问题，解题时应认真分析，得出解答问题的途径是什么，从而解得问题，是基础题．
练习册系列答案
课堂全解字词句段篇章系列答案
相关题目
用反证法证明命题“若a2m+b2n=0，（a，b∈R，且m，n∈N*），则a，b全为0”时，应假设（ ）
| A、a，b中至少有一个为0 |
| B、a，b中至少有一个不为0 |
| C、a，b全不为0 |
| D、a，b中只有一个为0 |
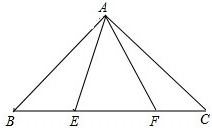在△ABC中，AB=AC，∠BAC=90°，点E，F在BC边上（不与B，C重合），∠EAF=45°，问以BE、EF、FC三条线段为边，是否总能构成直角三角形？请说明结论及理由．
如图，在四棱锥E-ABCD中，底面ABCD为正方形，AE⊥平面CDE，已知AE=DE=2，F为线段DE的中点．