题目内容
 将一块边长为a的正方形铁皮,剪去四个角(四个全等的正方形),作成一个无盖的铁盒,要使其容积最大,剪去的小正方形的边长为多少?最大容积是多少?
将一块边长为a的正方形铁皮,剪去四个角(四个全等的正方形),作成一个无盖的铁盒,要使其容积最大,剪去的小正方形的边长为多少?最大容积是多少?考点:基本不等式在最值问题中的应用,棱柱、棱锥、棱台的体积
专题:综合题,空间位置关系与距离
分析:首先由题意建立起无盖铁盒的体积函数,变形成为(a-2x)•(a-2x)•4x,分析得到其“和”是定值,联想到利用基本不等式求最值,即可得出结论.
解答:
解:设剪去的小正方形的边长为x,则无盖铁盒体积V=(a-2x)2•x.
所以:V=(a-2x)2•x=
(a-2x)•(a-2x)•4x≤
[
]3=
a3,
当且仅当a-2x=4x时,即x=
时取得最大值
a3.
所以:V=(a-2x)2•x=
| 1 |
| 4 |
| 1 |
| 4 |
| (a-2x)+(a-2x)+4x |
| 3 |
| 2 |
| 27 |
当且仅当a-2x=4x时,即x=
| a |
| 6 |
| 2 |
| 27 |
点评:此题主要考查利用基本不等式求最值在实际问题中的应用.前提是“一正二定三相等”,需通过变形技巧,得到“和”或“积”为定值的情形.然后应用不等式即可.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
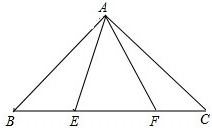 在△ABC中,AB=AC,∠BAC=90°,点E,F在BC边上(不与B,C重合),∠EAF=45°,问以BE、EF、FC三条线段为边,是否总能构成直角三角形?请说明结论及理由.
在△ABC中,AB=AC,∠BAC=90°,点E,F在BC边上(不与B,C重合),∠EAF=45°,问以BE、EF、FC三条线段为边,是否总能构成直角三角形?请说明结论及理由. 如图,在四棱锥E-ABCD中,底面ABCD为正方形,AE⊥平面CDE,已知AE=DE=2,F为线段DE的中点.
如图,在四棱锥E-ABCD中,底面ABCD为正方形,AE⊥平面CDE,已知AE=DE=2,F为线段DE的中点. 如图,已知在侧棱垂直于底面三棱柱ABC-A1B1C1中,AC=3,AB=5,BC=4,AA1=4,点D是AB的中点.
如图,已知在侧棱垂直于底面三棱柱ABC-A1B1C1中,AC=3,AB=5,BC=4,AA1=4,点D是AB的中点.