题目内容
对于曲线C:
+
=1给出下面四个命题:
①曲线C不可能表示椭圆
②当1<k<4时,曲线C表示椭圆
③若曲线C表示双曲线,则k<1或k>4
④若曲线C表示焦点在x 轴上的椭圆,则1<k<
下列选项正确的是( )
| x2 |
| 4-k |
| y2 |
| k-1 |
①曲线C不可能表示椭圆
②当1<k<4时,曲线C表示椭圆
③若曲线C表示双曲线,则k<1或k>4
④若曲线C表示焦点在x 轴上的椭圆,则1<k<
| 5 |
| 2 |
下列选项正确的是( )
| A、①③ | B、③④ | C、②③ | D、①④ |
考点:圆锥曲线的共同特征
专题:计算题,圆锥曲线的定义、性质与方程
分析:根据曲线方程的特点,结合椭圆双曲线的标准方程分别判断即可.
解答:
解:①当1<k<4且k≠
时,曲线表示椭圆,所以①错误;
②当k=
时,4-k=k-1,此时曲线表示圆,所以②错误.
③若曲线C表示双曲线,则(4-k)(k-1)<0,解得k>4或k<1,所以③正确.
④若曲线C表示焦点在x轴上的椭圆,则
,解得1<k<
,所以④正确.
故选B.
| 5 |
| 2 |
②当k=
| 5 |
| 2 |
③若曲线C表示双曲线,则(4-k)(k-1)<0,解得k>4或k<1,所以③正确.
④若曲线C表示焦点在x轴上的椭圆,则
|
| 5 |
| 2 |
故选B.
点评:本题主要考查圆锥曲线的方程,根据椭圆和双曲线的标准方程和定义是解决本题的关键.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
已知
,
都是单位向量,则下列结论正确的是( )
| a |
| b |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
设A={3,5,6,8},B={4,5,7,8},则A∩B=( )
| A、{3,4,5,6,7,8} |
| B、{5,8} |
| C、{3,6,7,4} |
| D、{3,5,8} |
若a>0,b>0,且2a+b=1,则S=
-4a2-b2的最大值为( )
| ab |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
用反证法证明命题“若a2m+b2n=0,(a,b∈R,且m,n∈N*),则a,b全为0”时,应假设( )
| A、a,b中至少有一个为0 |
| B、a,b中至少有一个不为0 |
| C、a,b全不为0 |
| D、a,b中只有一个为0 |
函数f(x)=-x2+2x+3在区间[-2,2]上的最大、最小值分别为( )
| A、4,3 | B、3,-5 |
| C、4,-5 | D、5,-5 |
满足f(x+π)=-f(x)且为奇函数的函数f(x)可能是( )
| A、cos2x | ||
| B、sinx | ||
C、sin
| ||
| D、cosx | ||
E、sin
|
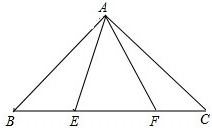 在△ABC中,AB=AC,∠BAC=90°,点E,F在BC边上(不与B,C重合),∠EAF=45°,问以BE、EF、FC三条线段为边,是否总能构成直角三角形?请说明结论及理由.
在△ABC中,AB=AC,∠BAC=90°,点E,F在BC边上(不与B,C重合),∠EAF=45°,问以BE、EF、FC三条线段为边,是否总能构成直角三角形?请说明结论及理由.