题目内容
已知△ABC中,AB=BC=AP=1,∠ABC=120°,∠APC=150°.
(1)求三角形APB的面积S;
(2)求sin∠BCP的值.
(1)求三角形APB的面积S;
(2)求sin∠BCP的值.
考点:正弦定理
专题:三角函数的求值,解三角形
分析:(1)先利用余弦定理求得AC,进而在△ACP中利用正弦定理求得sin∠ACP的值,利用平方关系求得cos∠ACP,然后根据sin∠PAC=sin(30°-∠ACP)利用正弦的两角和公式求得sin∠PAC的值,最后利用三角形面积公式求得答案.
(2)根据(1)中求得的sin∠ACP和cos∠ACP,根据sin∠BCP=sin(30°+∠ACP)利用两角和与差的正弦函数求得答案.
(2)根据(1)中求得的sin∠ACP和cos∠ACP,根据sin∠BCP=sin(30°+∠ACP)利用两角和与差的正弦函数求得答案.
解答:
解: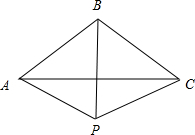
(1)在△ABC中,AC=
=
,
在△ACP中,由正弦定理知:
=
,
∴sin∠ACP=
=
=
,
∴cos∠ACP=
=
,
sin∠PAC=sin(30°-∠ACP)=sin30°cos∠ACP-cos30°sin∠ACP=
×
-
×
=
.
∴三角形面积S=
•AB•AP•sin∠PAC=
×1×1×
=
.
(2)sin∠BCP=sin(30°+∠ACP)=
×
+
×
=
.

(1)在△ABC中,AC=
| 1+1-2×1×1×cos120° |
| 3 |
在△ACP中,由正弦定理知:
| AP |
| sin∠ACP |
| AC |
| sin∠APC |
∴sin∠ACP=
| AP•sin∠APC |
| AC |
1×
| ||
|
| ||
| 6 |
∴cos∠ACP=
1-
|
| ||
| 6 |
sin∠PAC=sin(30°-∠ACP)=sin30°cos∠ACP-cos30°sin∠ACP=
| 1 |
| 2 |
| ||
| 6 |
| ||
| 2 |
| ||
| 6 |
| ||
| 12 |
∴三角形面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 12 |
| ||
| 24 |
(2)sin∠BCP=sin(30°+∠ACP)=
| 1 |
| 2 |
| ||
| 6 |
| ||
| 2 |
| ||
| 6 |
| ||
| 12 |
点评:本题主要考查了正弦定理和余弦定理的应用,三角形恒等变换的应用.解题的关键是求得sin∠ACP,以此为中介分别求得sin∠PAC和sin∠BCP.

练习册系列答案
相关题目
函数f(x)=-x2+2x+3在区间[-2,2]上的最大、最小值分别为( )
| A、4,3 | B、3,-5 |
| C、4,-5 | D、5,-5 |
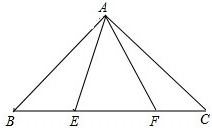 在△ABC中,AB=AC,∠BAC=90°,点E,F在BC边上(不与B,C重合),∠EAF=45°,问以BE、EF、FC三条线段为边,是否总能构成直角三角形?请说明结论及理由.
在△ABC中,AB=AC,∠BAC=90°,点E,F在BC边上(不与B,C重合),∠EAF=45°,问以BE、EF、FC三条线段为边,是否总能构成直角三角形?请说明结论及理由. 如图,已知在侧棱垂直于底面三棱柱ABC-A1B1C1中,AC=3,AB=5,BC=4,AA1=4,点D是AB的中点.
如图,已知在侧棱垂直于底面三棱柱ABC-A1B1C1中,AC=3,AB=5,BC=4,AA1=4,点D是AB的中点.