题目内容
7.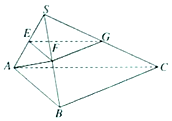 如图,在三棱锥S-ABC中,平面SAB⊥平面SBC,AB⊥BC,AS=AB,点E、F、G分别是棱SA、SB、SC的中点.求证:
如图,在三棱锥S-ABC中,平面SAB⊥平面SBC,AB⊥BC,AS=AB,点E、F、G分别是棱SA、SB、SC的中点.求证:(1)平面EFG∥平面ABC;
(2)BC⊥平面SAB.
分析 (1)证明EF∥平面ABC,EG∥平面ABC,即可证明平面EFG∥平面ABC;
(2)证明AF⊥平面SBC,可得AF⊥BC.又因为AB⊥BC,即可证明BC⊥平面SAB.
解答 证明:(1)因为F是SB的中点.又因为E是SA的中点,所以EF∥AB.
因为EF?平面ABC,AB?平面ABC,所以EF∥平面ABC.
同理EG∥平面ABC.又EF∩EG=E,
所以平面EFG∥平面ABC.…(6分)
(2)因为F是SB的中点,AS=AB,所以AF⊥SB…(8分)
因为平面SAB⊥平面SBC,且交线为SB,又AF?平面SAB,
所以AF⊥平面SBC.
又因为BC?平面SBC,所以AF⊥BC.
又因为AB⊥BC,AF∩AB=A,AF,AB?平面SAB,
所以BC⊥平面SAB.…(13分)
点评 本题考查线面、面面平行的判定,考查线面垂直的判定,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
15.过点A(1,2)且平行于直线3x+2y-1=0的直线方程为( )
| A. | 2x-3y+4=0 | B. | 3x-2y+1=0 | C. | 2x+3y-8=0 | D. | 3x+2y-7=0 |
19.已知两定点A(-2,0)和B(2,0),动点P(x,y)在直线l:y=x+4上移动,椭圆C以A,B为焦点且经过点P,则椭圆C的离心率的最大值为( )
| A. | $\frac{\sqrt{10}}{10}$ | B. | $\frac{\sqrt{10}}{5}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{2\sqrt{5}}{5}$ |
16.已知函数f(x)=2x-b(2≤x≤4,b为常数)的图象经过点(3,1),则f(x)的值域为( )
| A. | [4,16] | B. | [2,10] | C. | [$\frac{1}{2}$,2] | D. | [$\frac{1}{2}$,+∞) |