题目内容
19.已知两定点A(-2,0)和B(2,0),动点P(x,y)在直线l:y=x+4上移动,椭圆C以A,B为焦点且经过点P,则椭圆C的离心率的最大值为( )| A. | $\frac{\sqrt{10}}{10}$ | B. | $\frac{\sqrt{10}}{5}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{2\sqrt{5}}{5}$ |
分析 由题意知,要使椭圆C的离心率取最大值,则a取最小值.即|PA|+|PB|取最小值.利用点的对称性求出|PA|+|PB|的最小值即可解答本题.
解答 解:由题意得,
2c=|AB|=4.
∴c=2.
2a=|PA|+|PB|.
当a取最小值时,椭圆C的离心率有最大值.
设点A(-2,0)关于直线l:y=x+4的对称点为A′(x,y).
则$\left\{\begin{array}{l}{\frac{y}{x+2}=-1}\\{\frac{y}{2}=\frac{x-2}{2}+4}\end{array}\right.$.
解得,$\left\{\begin{array}{l}{x=-4}\\{y=2}\end{array}\right.$.
∴A′(-4,2).
则|PA|+|PB|=|PA′|+|PB|≥|A′B|.
∴2a≥|A′B|=$\sqrt{40}$=2$\sqrt{10}$.
∴当a=$\sqrt{10}$时,椭圆有最大离心率.
此时,$\frac{c}{a}$=$\frac{2}{\sqrt{10}}$$\frac{\sqrt{10}}{5}$.
故选:B.
点评 本题考查椭圆的基本性质,动点到定点距离的最值等知识,属于中档题.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
11.已知向量$\overrightarrow a$与向量$\overrightarrow b$满足|$\overrightarrow a$|=3,|$\overrightarrow b$|=2,|$2\overrightarrow a+\overrightarrow b$|=2$\sqrt{13}$,则$\overrightarrow a$与$\overrightarrow b$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
8.$\root{3}{(lg50-1)^{3}}$-$\sqrt{(lg2-1)^{2}}$=( )
| A. | 2lg5 | B. | 0 | C. | -1 | D. | -2lg5 |
16.若函数$f(x)=sin(\frac{1}{2}x+\frac{π}{6})$,则f(x)( )
| A. | 图象关于$x=\frac{π}{3}$对称 | |
| B. | 图象关于$(\frac{2π}{3},0)$对称 | |
| C. | 在$[\frac{2π}{3},\frac{8π}{3}]$上单调递减 | |
| D. | 单调递增区间是$[2kπ-\frac{4π}{3},2kπ+\frac{2π}{3}](k∈Z)$ |
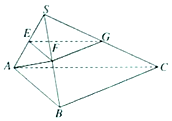 如图,在三棱锥S-ABC中,平面SAB⊥平面SBC,AB⊥BC,AS=AB,点E、F、G分别是棱SA、SB、SC的中点.求证:
如图,在三棱锥S-ABC中,平面SAB⊥平面SBC,AB⊥BC,AS=AB,点E、F、G分别是棱SA、SB、SC的中点.求证: