题目内容
15．过点A（1，2）且平行于直线3x+2y-1=0的直线方程为（ ）| A． | 2x-3y+4=0 | B． | 3x-2y+1=0 | C． | 2x+3y-8=0 | D． | 3x+2y-7=0 |
分析 设过点A（1，2）且平行于直线3x+2y-1=0的直线方程为3x+2y+m=0，把点A（1，2）代入上述方程解得m即可得出．
解答 解：设过点A（1，2）且平行于直线3x+2y-1=0的直线方程为3x+2y+m=0，
把点A（1，2）代入上述方程可得：3+4+m=0，解得m=-7．
∴要求的直线方程为：3x+2y-7=0．
故选：D．
点评 本题考查了相互平行的直线斜率之间的关系，考查了推理能力与计算能力，属于基础题．
练习册系列答案
相关题目
5．命题p：甲的数学成绩不低于100分，命题q：乙的数字成绩低于100分，则p∨（￢q）表示（ ）
| A． | 甲、乙两人数学成绩都低于100分 | |
| B． | 甲、乙两人至少有一人数学成绩低于100分 | |
| C． | 甲、乙两人数学成绩都不低于100分 | |
| D． | 甲、乙两人至少有一人数学成绩不低于100分 |
6．
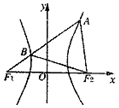如图，F1、F2是双曲线$\frac{x^2}{9}-\frac{y^2}{b^2}=1（b＞0）$的左、右焦点，过F1的直线l与双曲线分别交于点A、B，若△ABF2为等边三角形，则△BF1F2的面积为（ ）
如图，F1、F2是双曲线$\frac{x^2}{9}-\frac{y^2}{b^2}=1（b＞0）$的左、右焦点，过F1的直线l与双曲线分别交于点A、B，若△ABF2为等边三角形，则△BF1F2的面积为（ ）| A． | $8\sqrt{3}$ | B． | $9\sqrt{3}$ | C． | $18\sqrt{3}$ | D． | $27\sqrt{3}$ |
20．已知a＞1，f（x）=x2-ax，当x∈（-1，1）时，均有f（x）＜$\frac{2}{3}$，则实数a的取值范围是（ ）
| A． | （1，2） | B． | （1，3] | C． | （1，$\frac{3}{2}$） | D． | （1，2] |
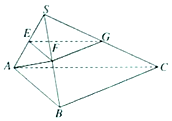如图，在三棱锥S-ABC中，平面SAB⊥平面SBC，AB⊥BC，AS=AB，点E、F、G分别是棱SA、SB、SC的中点．求证：