题目内容
20.《九章算术》是我国古代的数学名著,书中有如下问题:“今有五人分五钱,令上二人所得与下三人等.问各得几何.”其意思为“已知甲、乙、丙、丁、戊五人分5钱,甲、乙两人所得与丙、丁、戊三人所得相同,且甲、乙、丙、丁、戊所得依次成等差数列.问五人各得多少钱?”(“钱”是古代的一种重量单位).这个问题中,甲所得为( )| A. | $\frac{5}{4}$钱 | B. | $\frac{4}{3}$钱 | C. | $\frac{3}{2}$钱 | D. | $\frac{5}{3}$钱 |
分析 依题意设甲、乙、丙、丁、戊所得钱分别为a-2d,a-d,a,a+d,a+2d,由题意求得a=-6d,结合a-2d+a-d+a+a+d+a+2d=5a=5求得a=1,则答案可求.
解答 解:依题意设甲、乙、丙、丁、戊所得钱分别为a-2d,a-d,a,a+d,a+2d,
则由题意可知,a-2d+a-d=a+a+d+a+2d,即a=-6d,
又a-2d+a-d+a+a+d+a+2d=5a=5,∴a=1,
则a-2d=a-2×$(-\frac{a}{6})$=$\frac{4}{3}a=\frac{4}{3}$.
故选:B.
点评 本题考查等差数列的通项公式,是基础的计算题.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
15.若复数z满足iz=2-4i,则$\overline{z}$在复平面内对应的点的坐标是( )
| A. | (2,4) | B. | (2,-4) | C. | (-4,-2) | D. | (-4,2) |
5.某商场举行优惠促销活动,顾客仅可以从以下两种优惠方案中选择一种,
方案一:每满200元减50元:
方案二:每满200元可抽奖一次.具体规则是依次从装有3个红球、1个白球的甲箱,装有2个红球、2个白球的乙箱,以及装有1个红球、3个白球的丙箱中各随机摸出1个球,所得结果和享受的优惠如下表:(注:所有小球仅颜色有区别)
(Ⅰ)若两个顾客都选择方案二,各抽奖一次,求至少一个人获得半价优惠的概率;
(Ⅱ)若某顾客购物金额为320元,用所学概率知识比较哪一种方案更划算?
方案一:每满200元减50元:
方案二:每满200元可抽奖一次.具体规则是依次从装有3个红球、1个白球的甲箱,装有2个红球、2个白球的乙箱,以及装有1个红球、3个白球的丙箱中各随机摸出1个球,所得结果和享受的优惠如下表:(注:所有小球仅颜色有区别)
| 红球个数 | 3 | 2 | 1 | 0 |
| 实际付款 | 半价 | 7折 | 8折 | 原价 |
(Ⅱ)若某顾客购物金额为320元,用所学概率知识比较哪一种方案更划算?
9.已知函数f(x)=x3-ax2+4,若f(x)的图象与x轴正半轴有两个不同的交点,则实数a的取值范围为( )
| A. | (1,+∞) | B. | ($\frac{3}{2}$,+∞) | C. | (2,+∞) | D. | (3,+∞) |
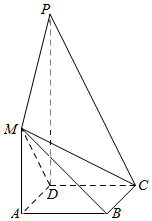 如图,正方形ABCD与梯形AMPD所在的平面互相垂直,AD⊥PD,MA∥PD,MA=AD=$\frac{1}{2}$PD=1.
如图,正方形ABCD与梯形AMPD所在的平面互相垂直,AD⊥PD,MA∥PD,MA=AD=$\frac{1}{2}$PD=1.