题目内容
9.已知函数f(x)=x3-ax2+4,若f(x)的图象与x轴正半轴有两个不同的交点,则实数a的取值范围为( )| A. | (1,+∞) | B. | ($\frac{3}{2}$,+∞) | C. | (2,+∞) | D. | (3,+∞) |
分析 利用参数分离法,进行转化,构造函数,求函数的导数,研究函数的极值即可得到结论.
解答 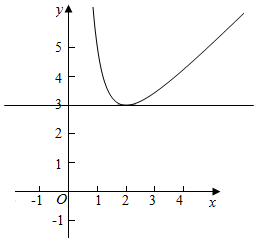 解:由题意可知f(x)=x3-ax2+4=0,即a=x+$\frac{4}{{x}^{2}}$有两个不等的正根,
解:由题意可知f(x)=x3-ax2+4=0,即a=x+$\frac{4}{{x}^{2}}$有两个不等的正根,
设h(x)=x+$\frac{4}{{x}^{2}}$,x>0,
则h′(x)=1-$\frac{8}{{x}^{3}}$=$\frac{{x}^{3}-8}{{x}^{3}}$,
令h′(x)=0,得x=2,
由h′(x)>0得x>2,此时函数单调递增,
由h′(x)<0得,0<x<2,此时函数单调递减,
即在x=2处取得极小值h(2)=2+$\frac{4}{{2}^{2}}$=2+1=3,
结合h(x)的图象可得a>3,
故选D
点评 本题主要考查函数与方程的应用,利用参数分离法,构造函数,研究函数的极值,结合数形结合是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.《九章算术》是我国古代的数学名著,书中有如下问题:“今有五人分五钱,令上二人所得与下三人等.问各得几何.”其意思为“已知甲、乙、丙、丁、戊五人分5钱,甲、乙两人所得与丙、丁、戊三人所得相同,且甲、乙、丙、丁、戊所得依次成等差数列.问五人各得多少钱?”(“钱”是古代的一种重量单位).这个问题中,甲所得为( )
| A. | $\frac{5}{4}$钱 | B. | $\frac{4}{3}$钱 | C. | $\frac{3}{2}$钱 | D. | $\frac{5}{3}$钱 |
4.已知a,b∈R,则“a>0,b>0”是“a2+b2≥2ab”的( )
| A. | 既不充分也不要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 充分必要条件 |
14.如图所示,使电路接通,开关不同的开闭方式共有( )
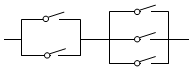

| A. | 11 | B. | 12 | C. | 20 | D. | 21 |
1.函数$f(x)=sin2x+\sqrt{3}cos2x$的最小正周期为( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | π | D. | 2π |
18.已知集合A={x|-2<x<3},B={x|log2x>1},则A∩(∁RB)=( )
| A. | (-2,2] | B. | (-2,1] | C. | (0,3) | D. | (1,3) |