题目内容
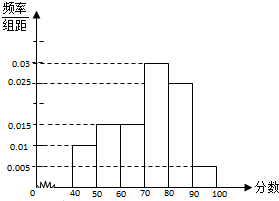 某校从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六组[40,50),[50,60)…[90,100]后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
某校从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六组[40,50),[50,60)…[90,100]后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:(Ⅰ)求成绩落在[70,80)上的频率,并补全这个频率分布直方图;
(Ⅱ) 根据直方图估计这次考试的及格率(60分及以上为及格)和平均分;
(Ⅲ) 若参加考试的学生共有600人,估计本次考试70分以上的学生共有多少人?
考点:频率分布直方图
专题:概率与统计
分析:(Ⅰ)由小长方形的面积是该组的频率求出落在[70,80)上的频率,再由频率之和是1补全频率分布直方图;
(Ⅱ)由对立事件的概率公式求出这次考试的及格率,再由加权平均数求出平均分的估计值;
(Ⅲ)根据图和频率公式求出本次考试70分以上的学生的人数.
(Ⅱ)由对立事件的概率公式求出这次考试的及格率,再由加权平均数求出平均分的估计值;
(Ⅲ)根据图和频率公式求出本次考试70分以上的学生的人数.
解答:
 解:(Ⅰ)成绩落在[70,80)上的频率是0.03×10=0.3,
解:(Ⅰ)成绩落在[70,80)上的频率是0.03×10=0.3,
频率分布直方图如图:
-----------------------------------------------3分
(Ⅱ) 估计这次考试的
及格率(60分及以上为及格)为:1-0.01×10-0.015×10=75%
平均分:45×0.1+55×0.15+65×0.15+75×0.3+85×0.25+95×0.05=71----------9分
(Ⅲ) 成绩是70分以上(包括70分)的学生人数为
(0.03+0.025+0.005)×10×600=360-----------------------12分.
 解:(Ⅰ)成绩落在[70,80)上的频率是0.03×10=0.3,
解:(Ⅰ)成绩落在[70,80)上的频率是0.03×10=0.3,频率分布直方图如图:
-----------------------------------------------3分
(Ⅱ) 估计这次考试的
及格率(60分及以上为及格)为:1-0.01×10-0.015×10=75%
平均分:45×0.1+55×0.15+65×0.15+75×0.3+85×0.25+95×0.05=71----------9分
(Ⅲ) 成绩是70分以上(包括70分)的学生人数为
(0.03+0.025+0.005)×10×600=360-----------------------12分.
点评:本题考查频率分布直方图中频率的性质,加权平均数、频率公式的应用,属于基础题.

练习册系列答案
相关题目
函数f(x)=3x+log2x的零点所在区间为( )
A、[
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
已知奇函数f(x)在定义域[-1,1]上为增函数,且f(
)+f(2x-1)>0,则x的取值范围是( )
| x |
| 2 |
A、(
| ||
B、(
| ||
C、(
| ||
| D、[0,2] |