题目内容
函数f(x)=3x+log2x的零点所在区间为( )
A、[
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
考点:函数零点的判定定理
专题:计算题,函数的性质及应用
分析:首先判断函数f(x)=3x+log2x是定义域上的增函数,再利用函数的零点判断.
解答:
解:易知函数f(x)=3x+log2x是定义域上的增函数,
f(
)=
-2<0;
f(
)=
-1>0;
故函数f(x)=3x+log2x的零点所在区间为[
,
];
故选C.
f(
| 1 |
| 4 |
| 3 |
| 4 |
f(
| 1 |
| 2 |
| 3 |
| 2 |
故函数f(x)=3x+log2x的零点所在区间为[
| 1 |
| 4 |
| 1 |
| 2 |
故选C.
点评:本题考查了函数的零点的判断,属于基础题.

练习册系列答案
相关题目
已知角α终边上一点P(
,1),则2sin2α-3tanα=( )
| 3 |
A、-1-3
| ||
B、1-3
| ||
C、-2
| ||
| D、0 |
已知函数y=
cos(x+
)的图象为C,为了得到函数y=
cos(x-
)的图象只需把C上所有的点( )
| 1 |
| 3 |
| π |
| 7 |
| 1 |
| 3 |
| π |
| 7 |
A、向右平行移动
| ||
B、向左平行移动
| ||
C、向右平行移动
| ||
D、向左平行移动
|
函数f(x)=log3(
)的图象关于( )
| 1-x |
| 1+x |
| A、y轴对称 | B、x轴对称 |
| C、原点对称 | D、直线y=x对称 |
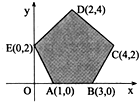 已知以x,y为自变量的目标函数ω=kx+y(k>0)的可行域如图阴影部分(含边界),若使ω取最大值时的最优解有无穷多个,则k的值为( )
已知以x,y为自变量的目标函数ω=kx+y(k>0)的可行域如图阴影部分(含边界),若使ω取最大值时的最优解有无穷多个,则k的值为( )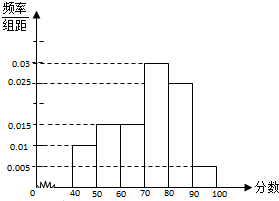 某校从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六组[40,50),[50,60)…[90,100]后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
某校从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六组[40,50),[50,60)…[90,100]后画出如下部分频率分布直方图.观察图形的信息,回答下列问题: