题目内容
(几何法)已知圆x2+y2+x-6y+m=0和直线x+2y-3=0交于P、Q两点,且OP⊥OQ(O为坐标原点),求该圆的圆心坐标及半径.
考点:直线与圆的位置关系
专题:直线与圆
分析:根据圆x2+y2+x-6y+m=0求出圆心C坐标及半径,设P、Q两点的中点A的坐标是(a,b),由弦的中点的性质列出方程组求出a、b,代入两点间的距离公式求出OA,再由OP⊥OQ和直角三角形的性质求出PQ,利用弦长公式求出半径r、m即可.
解答:
解:由圆x2+y2+x-6y+m=0得,圆心C坐标为(-
,3),半径r2=
-m>0,
设P、Q两点的中点A的坐标是(a,b),
因为PQ是圆x2+y2+x-6y+m=0的弦,所以CA⊥PQ,
则
,解得a=-1、b=2,
所以P、Q两点的中点A的坐标是(-1,2),则OA=
=
,
因为OP⊥OQ,所以PQ=2OA=2
,
因为圆心C到直线x+2y-3=0的距离d=
=
,
则由弦长公式得,r2=(
)2+(
)2=
-m,解得r=
,且m=3,
所以该圆的圆心坐标是(-
,3),半径r=
.
| 1 |
| 2 |
| 37 |
| 4 |
设P、Q两点的中点A的坐标是(a,b),
因为PQ是圆x2+y2+x-6y+m=0的弦,所以CA⊥PQ,
则
|
所以P、Q两点的中点A的坐标是(-1,2),则OA=
| 1+4 |
| 5 |
因为OP⊥OQ,所以PQ=2OA=2
| 5 |
因为圆心C到直线x+2y-3=0的距离d=
|-
| ||
|
| ||
| 2 |
则由弦长公式得,r2=(
| ||
| 2 |
| 5 |
| 37 |
| 4 |
| 5 |
| 2 |
所以该圆的圆心坐标是(-
| 1 |
| 2 |
| 5 |
| 2 |
点评:本题考查直线与圆的位置关系,圆的一般方程的求圆心、半径,弦长公式、弦的中点的性质,直角三角形的性质等,体现了几何法的应用,是常考题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知角α终边上一点P(
,1),则2sin2α-3tanα=( )
| 3 |
A、-1-3
| ||
B、1-3
| ||
C、-2
| ||
| D、0 |
设x,y满足约束条件
,则z=
的最大值为( )
|
| x2+y2 |
A、
| ||
| B、13 | ||
C、2
| ||
| D、8 |
 如图,在正三棱柱ABC-A1B1C1中,若各条棱长均为2,且M为A1C1的中点,则三棱锥M-AB1C的体积是
如图,在正三棱柱ABC-A1B1C1中,若各条棱长均为2,且M为A1C1的中点,则三棱锥M-AB1C的体积是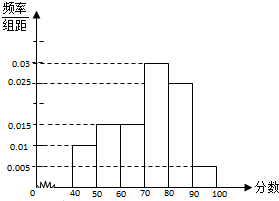 某校从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六组[40,50),[50,60)…[90,100]后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
某校从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六组[40,50),[50,60)…[90,100]后画出如下部分频率分布直方图.观察图形的信息,回答下列问题: