题目内容
设函数f(x)是定义在R上的偶函数.若当x≥0时,f(x)=
(1)当0<a<b时,若f(a)=f(b),则ab的取值范围 ;
(2)若关于x的方程f2(x)+bf(x)+c=0有7个不同实数解,则b,c满足的条件 .
|
|
(1)当0<a<b时,若f(a)=f(b),则ab的取值范围
(2)若关于x的方程f2(x)+bf(x)+c=0有7个不同实数解,则b,c满足的条件
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:(1)因为0<a<b,所以f(a)=f(b)建立等式关系,然后利用基本不等式即可求出ab的范围;
(2)根据图象可知对于方程f(x)=a,当a=0时,方程有3个根;当0<a<1时,方程有4个根,当a≥1时,方程有2个根;当a<0时,方程无解,则要使关于x的方程f2(x)+bf(x)+c=0有7个不同实数解,关于f(x)的方程f2(x)+bf(x)+c=0有一个在区间(0,1)的正实数根和一个等于零的根,即可求出b、c满足的条件.
(2)根据图象可知对于方程f(x)=a,当a=0时,方程有3个根;当0<a<1时,方程有4个根,当a≥1时,方程有2个根;当a<0时,方程无解,则要使关于x的方程f2(x)+bf(x)+c=0有7个不同实数解,关于f(x)的方程f2(x)+bf(x)+c=0有一个在区间(0,1)的正实数根和一个等于零的根,即可求出b、c满足的条件.
解答:
解:若x<0,在-x>0,则f(-x)=|1+
|,
∵函数f(x)是定义在R上的偶函数,
∴f(-x)=|1+
|=f(x),
即f(x)=|1+
|,x<0,
作出函数f(x)的图象如图:
(1)∵0<a<b,∴f(a)=f(b),
即|1-
|=|1-
|,整理得
+
=2,
即a+b=2ab>2
,
解得ab>1,
解得ab的取值范围是(1,+∞).
(2)由图象可知对于方程f(x)=a,当a=0时,方程有3个根;
当0<a<1时,方程有4个根,
当a≥1时,方程有2个根;当a<0时,方程无解
∴要使关于x的方程f2(x)+bf(x)+c=0有7个不同实数解,关于f(x)的方程f2(x)+bf(x)+c=0有一个在区间(0,1)的正实数根和一个等于零的根.
∴c=0,f(x)=-b∈(0,1),
即-1<b<0,c=0.
故答案为:(1).(1,+∞).(2).-1<b<0,c=0.
| 1 |
| x |
∵函数f(x)是定义在R上的偶函数,
∴f(-x)=|1+
| 1 |
| x |
即f(x)=|1+
| 1 |
| x |

作出函数f(x)的图象如图:
(1)∵0<a<b,∴f(a)=f(b),
即|1-
| 1 |
| a |
| 1 |
| b |
| 1 |
| a |
| 1 |
| b |
即a+b=2ab>2
| ab |
解得ab>1,
解得ab的取值范围是(1,+∞).
(2)由图象可知对于方程f(x)=a,当a=0时,方程有3个根;
当0<a<1时,方程有4个根,
当a≥1时,方程有2个根;当a<0时,方程无解
∴要使关于x的方程f2(x)+bf(x)+c=0有7个不同实数解,关于f(x)的方程f2(x)+bf(x)+c=0有一个在区间(0,1)的正实数根和一个等于零的根.
∴c=0,f(x)=-b∈(0,1),
即-1<b<0,c=0.
故答案为:(1).(1,+∞).(2).-1<b<0,c=0.
点评:本题主要考查函数零点个数的判断,利用换元法将方程转化为一元二次方程,利用数形结合是解决此类问题的基本方法.综合性较强,难度较大.

练习册系列答案
相关题目
设x,y满足约束条件
,则z=
的最大值为( )
|
| x2+y2 |
A、
| ||
| B、13 | ||
C、2
| ||
| D、8 |
不等式组
表示的平面区域的面积为( )
|
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f(x)=1+x-
+
-
+…+
,则下列结论正确的是( )
| x2 |
| 2 |
| x3 |
| 3 |
| x4 |
| 4 |
| x2015 |
| 2015 |
| A、f(x)在(0,1)上恰有一个零点 |
| B、f(x)在(-1,0)上恰有一个零点 |
| C、f(x)在(0,1)上恰有两个零点 |
| D、f(x)在(-1,0)上恰有两个零点 |
函数y=cos2x+sinxcosx的最小正周期T=( )
| A、π | ||
| B、2π | ||
C、
| ||
D、
|
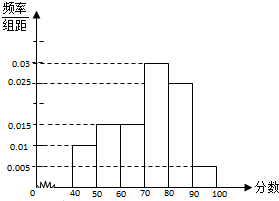 某校从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六组[40,50),[50,60)…[90,100]后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
某校从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六组[40,50),[50,60)…[90,100]后画出如下部分频率分布直方图.观察图形的信息,回答下列问题: