题目内容
设集合M={x|
+
=
+
}，N={x|
+
=
+
}，则M∩N= ．
| x-2 |
| 3 |
| x-3 |
| 2 |
| 3 |
| x-2 |
| 2 |
| x-3 |
| x-6 |
| 5 |
| x-5 |
| 6 |
| 5 |
| x-6 |
| 6 |
| x-5 |
考点：交集及其运算
专题：集合
分析：解方程求出集合M，N即可．
解答：
解：由
+
=
+
得
=
，
即
=
，即5x-13=0或x2-5x+6=6，
解得x=0或x=5或x=
，即M={0，5，
，}，
同理解得N={0，11，
}，
则M∩N={0}，
故答案为：{0}．
| x-2 |
| 3 |
| x-3 |
| 2 |
| 3 |
| x-2 |
| 2 |
| x-3 |
| 2(x-2)+3(x-3) |
| 6 |
| 3(x-3)+2(x-2) |
| (x-2)(x-3) |
即
| 5x-13 |
| 6 |
| 5x-13 |
| x2-5x+6 |
解得x=0或x=5或x=
| 13 |
| 5 |
| 13 |
| 5 |
同理解得N={0，11，
| 61 |
| 11 |
则M∩N={0}，
故答案为：{0}．
点评：本题主要考查集合的基本运算，根据方程求出集合M，N是解决本题的关键．
练习册系列答案
相关题目
正整数指数函数y=（a+1）x是x∈N上的减函数，则a的取值范围是（ ）
| A、0＜a＜1 | B、-1＜a＜0 |
| C、a＞0 | D、a≥0 |
函数f（x）=
的定义域是（ ）
| 1 | ||
|
| A、（0，+∞） |
| B、[0，+∞） |
| C、[3，+∞） |
| D、（3，+∞） |
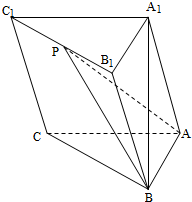如图，在三棱柱ABC-A1B1C1中，A1B⊥平面ABC，AB⊥AC．