题目内容
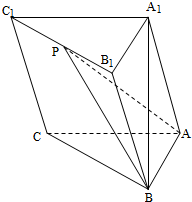 如图,在三棱柱ABC-A1B1C1中,A1B⊥平面ABC,AB⊥AC.
如图,在三棱柱ABC-A1B1C1中,A1B⊥平面ABC,AB⊥AC.(Ⅰ)求证:AC⊥BB1;
(Ⅱ)若P是棱B1C1的中点,求平面PAB将三棱柱ABC-A1B1C1分成的两部分体积之比.撸啊.
考点:棱柱、棱锥、棱台的体积,空间中直线与直线之间的位置关系
专题:空间位置关系与距离
分析:(Ⅰ)由已知得平面ABB1A1⊥平面ABC,从而AB⊥AC,进而AC⊥平面ABB1A1,由此能证明AC⊥BB1.
(Ⅱ)设平面PAB与棱A1C1交于Q,连结AQ,PQ,将棱台C1PQ-ABC还原为棱锥S-ABC,由此能求出平面PAB将三棱柱ABC-A1B1C1分成的两部分体积之比.
(Ⅱ)设平面PAB与棱A1C1交于Q,连结AQ,PQ,将棱台C1PQ-ABC还原为棱锥S-ABC,由此能求出平面PAB将三棱柱ABC-A1B1C1分成的两部分体积之比.
解答:
 (Ⅰ)证明:在三棱柱ABC-A1B1C1中,
(Ⅰ)证明:在三棱柱ABC-A1B1C1中,
∵A1B⊥平面ABC,A1B?平面ABB1,
∴平面ABB1A1⊥平面ABC,
∵平面ABB1A1∩平面ABC=AB,AB⊥AC,
∴AC⊥平面ABB1A1,
∴AC⊥BB1.
(Ⅱ)解:设平面PAB与棱A1C1交于Q,
∵P为棱B1C1的中点,∴Q为棱A1C1的中点,
连结AQ,PQ,
设三棱柱ABC-A1B1C1的底面积为S,高为h,体积为V,
则Sh=V,
如图,将棱台C1PQ-ABC还原为棱锥S-ABC,
解得VPQC1-ABC=
V,
VAB-A1B1PQ=V-
V=
V,
∴平面PAB将三棱柱ABC-A1B1C1分成的两部分体积之比为:
=
.
 (Ⅰ)证明:在三棱柱ABC-A1B1C1中,
(Ⅰ)证明:在三棱柱ABC-A1B1C1中,∵A1B⊥平面ABC,A1B?平面ABB1,
∴平面ABB1A1⊥平面ABC,
∵平面ABB1A1∩平面ABC=AB,AB⊥AC,
∴AC⊥平面ABB1A1,
∴AC⊥BB1.
(Ⅱ)解:设平面PAB与棱A1C1交于Q,
∵P为棱B1C1的中点,∴Q为棱A1C1的中点,
连结AQ,PQ,
设三棱柱ABC-A1B1C1的底面积为S,高为h,体积为V,
则Sh=V,
如图,将棱台C1PQ-ABC还原为棱锥S-ABC,
解得VPQC1-ABC=
| 7 |
| 12 |
VAB-A1B1PQ=V-
| 7 |
| 12 |
| 5 |
| 12 |
∴平面PAB将三棱柱ABC-A1B1C1分成的两部分体积之比为:
| VPQC1-ABC |
| VAB-A1B1PQ |
| 7 |
| 5 |
点评:本题考查异面直线垂直的证明,考查两个几何体的体积之比的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
若p:α=
,q:cos(
+α)=
,那么p是q的( )
| π |
| 6 |
| 3π |
| 2 |
| 1 |
| 2 |
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、非充分非必要条件 |
| D、充要条件 |
下列函数经过原点的是( )
| A、y=2x-1 |
| B、y=x-1 |
| C、y=log2x |
| D、y=-x2+1 |
设全集U={1,2,3,4},集合A={1,2,3},则∁UA=( )
| A、{1,2,3,4} |
| B、{1,2} |
| C、{4} |
| D、{1,2,4} |
 如图,在正三棱柱ABC-A1B1C1中,点D为棱AB的中点,BC=1,AA1=
如图,在正三棱柱ABC-A1B1C1中,点D为棱AB的中点,BC=1,AA1= 已知正方体ABCD-A1B1C1D1的棱长为2,M、N分别为AD、CC1的中点,O为上底面A1B1C1D1的中心,则三棱锥O-MNB的体积是
已知正方体ABCD-A1B1C1D1的棱长为2,M、N分别为AD、CC1的中点,O为上底面A1B1C1D1的中心,则三棱锥O-MNB的体积是