题目内容
3.已知{an}为等比数列,且a2=6,6a1+a3=30,求{an}的前n项和公式Sn.分析 设出等比数列的公比为q,然后根据等比数列的通项公式化简已知得两等式,得到关于首项与公比的二元一次方程组,求出方程组的解即可得到首项和公比的值,根据首项和公比写出相应的前n项和即可.
解答 解:设{an}的公比为q,由题意得:$\left\{\begin{array}{l}{{a}_{1}q=6}\\{6{a}_{1}+{a}_{1}{q}^{2}=30}\end{array}\right.$,
解得:a1=3,q=2或a1=2,q=3,
当a1=3,q=2时:Sn=$\frac{3(1-{2}^{n})}{1-2}$=3×(2n-1);
当a1=2,q=3时:Sn=$\frac{2(1-{3}^{n})}{1-3}$=3n-1.
点评 此题考查学生灵活运用等比数列前n项和的公式化简求值,是一道基础题.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
8.已知m,n是两条互相垂直的直线,α是平面,则n∥α是m⊥α的( )条件.
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充要 | D. | 既不充分也不必要 |
8.下列四个数中最大的是( )
| A. | (ln2)2 | B. | ln(ln2) | C. | ln$\sqrt{2}$ | D. | ln2 |
15.函数$y=\frac{1}{x+1}$的减区间是( )
| A. | (-1,+∞) | B. | (-∞,-1) | C. | (-∞,-1)∪(-1,+∞) | D. | (-∞,-1),(-1,+∞) |
12.下列说法中正确的是( )
| A. | 有两个面平行,其余各面都是三角形的几何体叫棱柱 | |
| B. | 有两个面平行,其余各面都是梯形的几何体叫棱台 | |
| C. | 有一个面是多边形,其余各面都是五边形的几何体叫棱锥 | |
| D. | 棱台各侧棱的延长线交于一点 |
13.若复数z满足iz=1+3i,则复数z的虚部为( )
| A. | -1 | B. | -i | C. | 1 | D. | i |
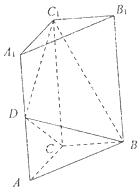 如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=$\frac{1}{2}$AA1=1,D是棱AA1上的点,DC1⊥BD
如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=$\frac{1}{2}$AA1=1,D是棱AA1上的点,DC1⊥BD