题目内容
8.侧棱与底面垂直的三棱柱ABC-A1B1C1的所有棱长均为2,则三棱锥B-AB1C的体积为$\frac{2\sqrt{3}}{3}$.分析 三棱锥B-AB1C的体积${V}_{B-A{B}_{1}C}$=${V}_{{B}_{1}-ABC}$,由此能求出三棱锥B-AB1C的体积.
解答 解: 如图,侧棱与底面垂直的三棱柱ABC-A1B1C1的所有棱长均为2,
如图,侧棱与底面垂直的三棱柱ABC-A1B1C1的所有棱长均为2,
∴${S}_{△ABC}=\frac{1}{2}×2×2×sin60°$=$\sqrt{3}$,AA1=2,
∴三棱锥B-AB1C的体积:
${V}_{B-A{B}_{1}C}$=${V}_{{B}_{1}-ABC}$=$\frac{1}{3}×A{A}_{1}×{S}_{△ABC}$
=$\frac{1}{3}×2×\sqrt{3}$=$\frac{2\sqrt{3}}{3}$.
故答案为:$\frac{2\sqrt{3}}{3}$.
点评 本题考查三棱锥体积的求法,考查棱锥性质、空间中线线、线面、面面间关系等基础知识,考查推理论证能力、运算求解能力、空间想象能力,考查化归与转化思想、函数与方程思想、数形结合思想,考查创新意识、应用意识,是中档题.

练习册系列答案
相关题目
3.已知全集U=Z,A={x|x2-x-2<0,x∈Z},B={-1,0,1,2},则(∁UA)∩B等于( )
| A. | {-1,2} | B. | {-1,0} | C. | {0,1} | D. | {1,2} |
13.若复数z满足iz=1+3i,则复数z的虚部为( )
| A. | -1 | B. | -i | C. | 1 | D. | i |
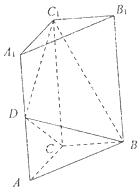 如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=$\frac{1}{2}$AA1=1,D是棱AA1上的点,DC1⊥BD
如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=$\frac{1}{2}$AA1=1,D是棱AA1上的点,DC1⊥BD