题目内容
7.已知p:?x∈[1,2],x2-a≥0,q:方程x2+2ax+2-a=0有实数解,若p且q为真命题,则实数a的取值范围是( )| A. | a≤-2或a=1 | B. | a≤2或1≤a≤2 | C. | a≥1 | D. | -2≤a≤1 |
分析 先求出命题p,q下的a的取值:由命题p得,a≤x2,所以只要让a小于等于x2的最小值即可;由命题q得,△≥0,这样即可求得命题p,q下的a的取值.根据p且q为真命题,得到p,q都是真命题,所以对在命题p,q下求得的a的取值求交集即可.
解答 解:命题p:?x∈[1,2],x2-a≥0,
∴a≤x2,
∵x2在[1,2]上的最小值为1,
∴a≤1;
命题q:方程x2+2ax+2-a=0有实数根;
∴△=4a2-4(2-a)≥0,解得a≤-2,或a≥1;
∵p且q为真命题,
∴p,q都是真命题.
∴a的取值范围是$\left\{\begin{array}{l}{a≤1}\\{a≤-2或a≥1}\end{array}\right.$
即a∈{a|a≤-2,或a=1}.
故选A.
点评 本题考查不等式恒成立问题转化为求二次函数在闭区间上的最值的求法,一元二次方程的根和判别式的关系,以及逻辑连接词的定义,及由逻辑连接词连接的命题的真假情况,考查运算能力和判断能力,属于中档题.

练习册系列答案
相关题目
14.为丰富少儿文体活动,某学校从篮球,足球,排球,橄榄球中任选2种球给甲班学生使用,剩余的2种球给乙班学生使用,则篮球和足球不在同一班的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
15.函数$y=\frac{1}{x+1}$的减区间是( )
| A. | (-1,+∞) | B. | (-∞,-1) | C. | (-∞,-1)∪(-1,+∞) | D. | (-∞,-1),(-1,+∞) |
12.下列说法中正确的是( )
| A. | 有两个面平行,其余各面都是三角形的几何体叫棱柱 | |
| B. | 有两个面平行,其余各面都是梯形的几何体叫棱台 | |
| C. | 有一个面是多边形,其余各面都是五边形的几何体叫棱锥 | |
| D. | 棱台各侧棱的延长线交于一点 |
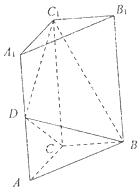 如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=$\frac{1}{2}$AA1=1,D是棱AA1上的点,DC1⊥BD
如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=$\frac{1}{2}$AA1=1,D是棱AA1上的点,DC1⊥BD