题目内容
空间直角坐标系中，已知A（2，3，5），B（3，1，4），则A，B两点间的距离为（ ）
| A、6 | ||
B、
| ||
C、
| ||
D、
|
考点：空间两点间的距离公式
专题：空间位置关系与距离
分析：根据所给的两个点的坐标，代入空间中两点之间的距离的公式，整理成最简结果，得到要求的A与B之间的距离，注意数字运算不要出错．
解答：
解：∵A，B两点的坐标分别是A（2，3，5），B（3，1，4），
∴|AB|=
=
，
故选：B．
∴|AB|=
| (3-2)2+(1-3)2+(4-5)2 |
| 6 |
故选：B．
点评：本题考查空间两点之间的距离公式，是一个基础题，这种题目是一些解析几何问题的题目的一个环节，一般不会单独出题．
练习册系列答案
名校课堂系列答案
相关题目
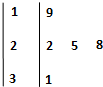已知某篮球运动员2013年度参加了25场比赛，若从中抽取5场，用茎叶图统计该运动员5场中的得分如图所示，则该样本的方差为 （ ）| A、4 | ||
B、
| ||
| C、18 | ||
| D、16 |
若函数f（x）=
cos（ωx+φ）对任意x∈R都有f（
-x）=f（
+x），则f（
）的值为（ ）
| 5 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
A、
| ||
B、-
| ||
C、±
| ||
| D、0 |
已知实数a，b满足-1≤a≤1，0≤b≤1，则函数f（x）=x3-ax2+bx无极值的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数y=f（x），将f（x）图象上每一点的纵坐标保持不变，横坐标扩大到原来的2倍，然后把所得到的图象沿x轴向左平移
个单位，这样得到的曲线与y=3sinx的图象相同，那么y=f（x）的解析式为（ ）
| π |
| 4 |
A、f（x）=3sin（
| ||||
B、f（x）=3sin（2x+
| ||||
C、f（x）=3sin（
| ||||
D、f（x）=3sin（2x-
|