题目内容
已知R是实数集，M={x|
＜1}，N={y|y=
}，则N∩∁R，N={y|y=
}，则N∩∁RM（ ）
| 2 |
| x |
| x-1 |
| x-1 |
| A、（1，2） | B、[0，2] |
| C、CϕD | D、[1，2] |
考点：交、并、补集的混合运算
专题：集合
分析：求出M中不等式的解集确定出M，求出N中y的范围确定出N，求出N与M补集的交集即可．
解答：
解：M中不等式
＜1，
当x＞0时，解得：x＞2；当x＜0时，解得：x＜2，即x＜0，
∴M=（-∞，0）∪（2，+∞），即∁RM=[0，2]，
由N中y=
≥0，得到N=[0，+∞），
则N∩∁RM=[0，2]．
故选：B．
| 2 |
| x |
当x＞0时，解得：x＞2；当x＜0时，解得：x＜2，即x＜0，
∴M=（-∞，0）∪（2，+∞），即∁RM=[0，2]，
由N中y=
| x-1 |
则N∩∁RM=[0，2]．
故选：B．
点评：此题考查了交、并、补集的混合运算，熟练掌握各自的定义是解本题的关键．
练习册系列答案
ABC考王全优卷系列答案
相关题目
某公司有5万元资金用于投资开发项目．如果成功，一年后可以获利12%；一旦失败，一年后将损失全部资金的50%．下表是过去200例类似项目开发的实施结果：
估计一年后该公司可获利（单位：万元）的期望值是（ ）
| 投资成功 | 投资失败 |
| 192例 | 8例 |
| A、0.676 |
| B、0.576 |
| C、0.476 |
| D、-0.01 |
点P与定点F（8，0）的距离和它到定直线x=2的距离的比是2，则点P的轨迹方程是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知复数z满足（1+i）
=3+i，z等于（ ）
. |
| z |
| A、2+i | B、2-i |
| C、-2-i | D、-2+i |
若幂函数f（x）=xm-1在（0，+∞）上是减函数，则（ ）
| A、m＞1 | B、不能确定 |
| C、m=l | D、m＜1 |
已知点O（0，0），A（1，2），B（3，0），以线段AB为直径作圆C，则直线l：x+y-4=0与圆C的位置关系是（ ）
| A、相切 | B、相离 |
| C、相交且过圆心 | D、相交但不过圆心 |
下列说法正确的是（ ）
A、向量
| ||||
| B、两个有共同起点长度相等的向量，则终点相同 | ||||
| C、零向量没有方向 | ||||
| D、任一向量与零向量平行 |
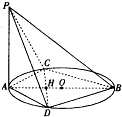已知AB是圆O的直径，C，D是圆上不同两点，且CD∩AB=H，AC=AD，PA⊥圆O所在平面