题目内容
设抛物线的顶点在原点,准线方程为x=-1,则抛物线的方程为 .
考点:抛物线的标准方程
专题:圆锥曲线的定义、性质与方程
分析:利用抛物线的简单性质求解.
解答:
解:∵抛物线的顶点在原点,准线方程为x=-1,
∴抛物线的方程为:y2=4x.
故答案为:y2=4x.
∴抛物线的方程为:y2=4x.
故答案为:y2=4x.
点评:本题考查抛物线的标准方程的求法,是基础题,解题时要注意抛物线的简单性质的合理运用.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
定义在R上的函数满足f(x)=f(x+2),当x∈[1,3]时,f(x)=2-|x-2|,则( )
A、f(sin
| ||||
| B、f (sin1)>f (cos1) | ||||
C、f(cos
| ||||
| D、f (cos2)>f (sin2) |
下列函数中,在区间(0,2)上为增函数的是( )
| A、y=2-x | ||
B、y=
| ||
C、y=-log
| ||
| D、y=-x2+2x+3 |
已知全集U=R,集合A={1,2,3,4,5},B={x∈R|
≤0},则A∩B=( )
| x+2 |
| x-3 |
| A、{1,2} |
| B、{x|-2≤x<3} |
| C、{x|0≤x<3} |
| D、{0,1} |
设{an}是等差数列,若a5=log
8,则a4+a6等于( )
2 |
| A、6 | B、8 | C、9 | D、16 |
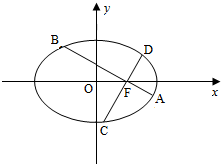 如图,在平面直角坐标系xOy中,椭圆
如图,在平面直角坐标系xOy中,椭圆