题目内容
(Ⅰ)已知2x+2-x=5,求4x+4-x的值;
(Ⅱ)化简2(
×
)6+(
)
-4(
)-
-
×80.25+(-2005)0.
(Ⅱ)化简2(
| 3 | 2 |
| 3 |
2
|
| 4 |
| 3 |
| 16 |
| 49 |
| 1 |
| 2 |
| 4 | 2 |
考点:有理数指数幂的化简求值
专题:函数的性质及应用
分析:(Ⅰ)由2x+2-x=5两边平方展开即可得出;
(II)利用指数幂的运算性质即可得出.
(II)利用指数幂的运算性质即可得出.
解答:
解:(Ⅰ)∵2x+2-x=5,∴25=(2x+2-x)2=4x+4-x+2,
∴4x+4-x=23.
(Ⅱ)原式=2(2
×3
)6+(2
×2
)
-4×
-2
×2
+1
=2×22×33+2-7-2+1
=210.
∴4x+4-x=23.
(Ⅱ)原式=2(2
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 4 |
| 3 |
| 7 |
| 4 |
| 1 |
| 4 |
| 3 |
| 4 |
=2×22×33+2-7-2+1
=210.
点评:本题考查了指数幂的运算性质、乘法公式,考查了计算能力,属于基础题.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
设{an}是等差数列,若a5=log
8,则a4+a6等于( )
2 |
| A、6 | B、8 | C、9 | D、16 |
已知a=log
3,b=log
2,c=20.3,则a,b,c三者的大小关系是( )
| 1 |
| 2 |
| 1 |
| 2 |
| A、c>b>a |
| B、a>c>b |
| C、b>a>c |
| D、c>a>b |
已知在正四面体ABCD中,E、F分别是线段AB和线段CD上一点,且AE=
AB,CF=
CD,则直线DE和BF所成角的余弦值是( )
| 1 |
| 4 |
| 1 |
| 4 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
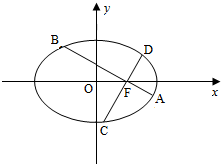 如图,在平面直角坐标系xOy中,椭圆
如图,在平面直角坐标系xOy中,椭圆