题目内容
函数y=|x-2|+|x+1|的最小值是 ．
考点：函数的最值及其几何意义
专题：函数的性质及应用,不等式的解法及应用
分析：利用绝对值的几何意义：在数轴上点x到点-1的距离加上点x到点2的距离．分析得当x在-1和2之间的时候，取最小值，即可得到答案．
解答：
解：在数轴上，设-1、2、x所对应的点分别是A、B、P，
则函数y=|x-2|+|x+1|的含义是P到A的距离与P到B的距离的和，
可以分析到当P在A和B之间的时候，距离和为线段AB的长度，此时最小．
即：y=|x-2|+|x+1|=|PA|+|PB|≥|AB|=3．
故答案为：3．
则函数y=|x-2|+|x+1|的含义是P到A的距离与P到B的距离的和，
可以分析到当P在A和B之间的时候，距离和为线段AB的长度，此时最小．
即：y=|x-2|+|x+1|=|PA|+|PB|≥|AB|=3．
故答案为：3．
点评：此题主要考查y=|x-a|+|x-b|此种类型的函数的最小值的求法，对于此种函数可以分析其几何意义，然后再求得最小值，难度一般．
练习册系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
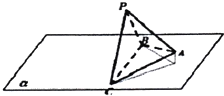我们把底面是正三角形，顶点在底面的射影是正三角形中心的三棱锥称为正三棱锥．现有一正三棱锥P-ABC放置在平面α上，已知它的底面边长为2，高为h，BC在平面α上，现让它绕BC转动，并使它在某一时刻在平面α上的射影是等腰直角三角形，则h的取值范围是在△ABC中，若cosA•cosB=sinA•sinB，则△ABC为（ ）
| A、锐角三角形 | B、直角三角形 |
| C、钝角三角形 | D、无法确定 |