题目内容
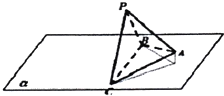 我们把底面是正三角形,顶点在底面的射影是正三角形中心的三棱锥称为正三棱锥.现有一正三棱锥P-ABC放置在平面α上,已知它的底面边长为2,高为h,BC在平面α上,现让它绕BC转动,并使它在某一时刻在平面α上的射影是等腰直角三角形,则h的取值范围是
我们把底面是正三角形,顶点在底面的射影是正三角形中心的三棱锥称为正三棱锥.现有一正三棱锥P-ABC放置在平面α上,已知它的底面边长为2,高为h,BC在平面α上,现让它绕BC转动,并使它在某一时刻在平面α上的射影是等腰直角三角形,则h的取值范围是考点:点、线、面间的距离计算,简单空间图形的三视图
专题:计算题,空间位置关系与距离
分析:分两类讨论,①当由点A在平面α内的射影与BC构成等腰直角三角形时,②当由点P在平面α内的射影与BC构成等腰直角三角形时;找到临界值,从而求出h的取值范围.
解答:
解:由正三棱锥在某一时刻在平面α上的射影是等腰直角三角形知,
①当由点A在平面α内的射影与BC构成等腰直角三角形时,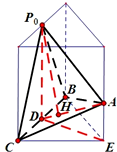
h可以趋近于0,但h变到最大时,面PBC⊥面α;
此时如右图,其中,A′A=
,A′D=1,DP′=
,
则由三角形相似可得,
=
;
则h=PP′=
=
,
则0<h≤
;
②当由点P在平面α内的射影与BC构成等腰直角三角形时,
点P在平面α内时,h最小,此时PD=1,则h=
=
;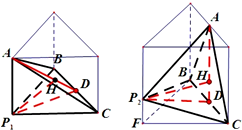
当面ABC⊥面α时,h最大,此时h=1.
则
≤h≤1.
综上所述,h的取值范围是:(0,
]∪[
,1].
故答案为:(0,
]∪[
,1].
①当由点A在平面α内的射影与BC构成等腰直角三角形时,

h可以趋近于0,但h变到最大时,面PBC⊥面α;
此时如右图,其中,A′A=
| 2 |
| ||
| 3 |
则由三角形相似可得,
| PP′ |
| DA′ |
| DP′ |
| AA′ |
则h=PP′=
| ||||
|
| ||
| 6 |
则0<h≤
| ||
| 6 |
②当由点P在平面α内的射影与BC构成等腰直角三角形时,
点P在平面α内时,h最小,此时PD=1,则h=
1-(
|
| ||
| 3 |

当面ABC⊥面α时,h最大,此时h=1.
则
| ||
| 3 |
综上所述,h的取值范围是:(0,
| ||
| 6 |
| ||
| 3 |
故答案为:(0,
| ||
| 6 |
| ||
| 3 |
点评:这是一道难度较高的题,考查点,线,面在一平面内的投影问题,是道压轴题,在解答时注意讨论分类,并找到临界图形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
以(1,1)和(2,-2)为一条直径的两个端点的圆的方程为( )
| A、x2+y2+3x-y=0 | ||
| B、x2+y2-3x+y=0 | ||
C、x2+y2-3x+y-
| ||
D、x2+y2-3x-y-
|