题目内容

在正项等比数列{an}中，2
2
为a4与a14的等比中项，则2a7+a11的最小值为（　　）
A、16B、8C、6D、4
考点：等比数列的性质
专题：计算题,等差数列与等比数列
分析：由各项为正的等比数列{an}中，a4与a14的等比中项为2
2
，知a4•a14=（2
2
）2=8，故a7•a11=8，利用均值不等式能够求出2a7+a11的最小值．
解答： 解：∵各项为正的等比数列{an}中，a4与a14的等比中项为2
2
，
∴a4•a14=（2
2
）2=8，
∴a7•a11=8，
∵a7＞0，a11＞0，
∴2a7+a11≥8．
故选B．
点评：本题考查等比数列的通项公式的应用，是中档题．解题时要认真审题，仔细解答．
练习册系列答案
相关题目
已知函数f（x）=2xcosx，则函数f（x）的部分图象可以为（　　）
A、
B、
C、
D、
已知f（x）是定义域为R的奇函数，当x≥0时，f（x）=2x-x-1，则x＜0时，f（x）的解析式为
 
．
下列对应中，是映射的个数为（　　）
A、0B、1C、2D、3
已知映射f：A→B，其中A=B=R，对应法则f：x→y=-x2+2x+1，对于实数k∈B，在集合A中存在不同的两个原象，则k的取值范围是
 
．
某算法程序框图如图所示，若a=
3
2
，b=3 
1
3
，c=log23，则x=（　　）
A、
a+b+c
3
B、a
C、b
D、c
设a∈R，则“a=1”是“直线l1：ax+（1-a）y=3”与直线l2：（a-1）x+（2a+3）y=2互相垂直的（　　）
A、充分不必要条件
B、必要不充分条件
C、充分必要条件
D、既不充分也不必要条件
已知全集U={1，2，3，4，5}，A={1，2，3}，B={3，4}，则∁U（A∪B）=
 
．
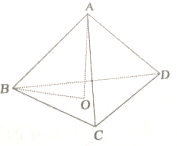如图，四面体ABCD中，AB、AC、AD两两垂直，若△BCD的垂心为O，求证：AO⊥平面BCD．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网