题目内容
已知f(x)是定义域为R的奇函数,当x≥0时,f(x)=2x-x-1,则x<0时,f(x)的解析式为 .
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:设x>0,则-x<0,由已知得f(-x)=2-x+x-1,由于f(x)是奇函数,可推出f(x)=-f(-x)=-(2-x+x-1)=-2-x-x+1.
解答:
解:设x>0,则-x<0,由已知得f(-x)=2-x-(-x)-1=2-x+x-1,
∵f(x)是奇函数,则x<0时,
∴f(x)=-f(-x)=-(2-x+x-1)=-2-x-x+1,
故答案为:f(x)=-2-x-x+1.
∵f(x)是奇函数,则x<0时,
∴f(x)=-f(-x)=-(2-x+x-1)=-2-x-x+1,
故答案为:f(x)=-2-x-x+1.
点评:本题重在考查函数的性质,关键是利用奇偶函数的性质解题,本题属于基础题.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目
设集合P={x|0≤x≤4},M={y|0≤y≤2},则下列表示P到M的映射的是( )
A、f:x→y=
| ||
B、f:x→y=
| ||
C、f:x→y=
| ||
D、f:x→y=
|
在正项等比数列{an}中,2
为a4与a14的等比中项,则2a7+a11的最小值为( )
| 2 |
| A、16 | B、8 | C、6 | D、4 |
排列数
=( )
| A | 3 5 |
| A、6 | B、20 | C、60 | D、120 |
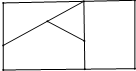 如图,用6种不同的颜色为一块广告牌着色,要求在四个区域中相邻的区域不用同一种颜色,则共有
如图,用6种不同的颜色为一块广告牌着色,要求在四个区域中相邻的区域不用同一种颜色,则共有