题目内容
设a∈R,则“a=1”是“直线l1:ax+(1-a)y=3”与直线l2:(a-1)x+(2a+3)y=2互相垂直的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:根据直线垂直得出a(a-1)+(1-a)(2a+3)=0,求出a=1或a=-3,再根据充分必要条件的定义可判断.
解答:
解:∵“直线l1:ax+(1-a)y=3”与直线l2:(a-1)x+(2a+3)y=2互相垂直,
∴a(a-1)+(1-a)(2a+3)=0,
即a=1或a=-3,
根据充分必要条件的定义可判断:
“a=1”是“直线l1:ax+(1-a)y=3”与直线l2:(a-1)x+(2a+3)y=2互相垂直的充分不必要条件,
故选:A
∴a(a-1)+(1-a)(2a+3)=0,
即a=1或a=-3,
根据充分必要条件的定义可判断:
“a=1”是“直线l1:ax+(1-a)y=3”与直线l2:(a-1)x+(2a+3)y=2互相垂直的充分不必要条件,
故选:A
点评:本题考查了直线的方程,位置关系,充分必要条件的定义属于容易题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设集合P={x|0≤x≤4},M={y|0≤y≤2},则下列表示P到M的映射的是( )
A、f:x→y=
| ||
B、f:x→y=
| ||
C、f:x→y=
| ||
D、f:x→y=
|
在正项等比数列{an}中,2
为a4与a14的等比中项,则2a7+a11的最小值为( )
| 2 |
| A、16 | B、8 | C、6 | D、4 |
已知cosθ<0,那么角θ是( )
| A、第一或第二象限角 |
| B、第三或第四象限角 |
| C、第二或第三象限角 |
| D、第一或第四象限角 |
排列数
=( )
| A | 3 5 |
| A、6 | B、20 | C、60 | D、120 |
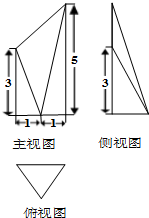 已知某几何体的三视图如图所示,其中俯视图是边长为2的正三角形,侧视图是直角三角形,则此几何体的体积为( )
已知某几何体的三视图如图所示,其中俯视图是边长为2的正三角形,侧视图是直角三角形,则此几何体的体积为( )A、
| ||||
B、
| ||||
C、8
| ||||
D、
|
