题目内容
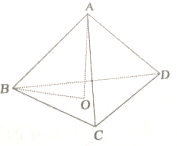如图，四面体ABCD中，AB、AC、AD两两垂直，若△BCD的垂心为O，求证：AO⊥平面BCD．考点：直线与平面垂直的判定
专题：空间位置关系与距离
分析：首先利用线线垂直得到线面垂直，进一步利用线面垂直得到线线垂直，最后得到线面垂直．
解答：
证明：四面体ABCD中，AB、AC、AD两两垂直
所以：AD⊥平面ABC
AD⊥BC①
又因为：△BCD的垂心为O
所以：DO⊥BC②
由①②得：BC⊥平面AOD
AO⊥BC
同理：AO⊥CD
所以：AO⊥平面BCD
所以：AD⊥平面ABC
AD⊥BC①
又因为：△BCD的垂心为O
所以：DO⊥BC②
由①②得：BC⊥平面AOD
AO⊥BC
同理：AO⊥CD
所以：AO⊥平面BCD
点评：本题考查的知识点：线面垂直的判定定理和性质定理，及线面垂直和线线垂直之间的转化．
练习册系列答案
活力课时同步练习册系列答案
学业测评一课一测系列答案
相关题目
在正项等比数列{an}中，2
为a4与a14的等比中项，则2a7+a11的最小值为（ ）
| 2 |
| A、16 | B、8 | C、6 | D、4 |
排列数
=（ ）
| A | 3 5 |
| A、6 | B、20 | C、60 | D、120 |
已知集合A={1，2，0，-2}，B={0，2，4}，则A∩B=（ ）
| A、{1，-2} |
| B、{0，2} |
| C、{0，1，2，4，-2} |
| D、{1，-2，4} |
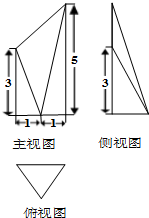已知某几何体的三视图如图所示，其中俯视图是边长为2的正三角形，侧视图是直角三角形，则此几何体的体积为（ ）A、
| ||||
B、
| ||||
C、8
| ||||
D、
|
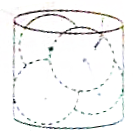如图，在底面直径为4r的圆柱内，正方放入4个半径为r的小球，使得圆柱上下表面与小球正好相切，则圆柱的高为