题目内容
 如图,点P为圆O的弦AB上的一点,连接PO,过点P作PC⊥OP,且PC交圆O于C.若AP=4,PC=2,则PB=
如图,点P为圆O的弦AB上的一点,连接PO,过点P作PC⊥OP,且PC交圆O于C.若AP=4,PC=2,则PB=考点:与圆有关的比例线段
专题:计算题,立体几何
分析:根据题设中的已知条件,利用相交弦定理,直接求解.
解答:
解:延长CP,交圆于D,则
∵AB是⊙O的一条弦,点P为AB上一点,PC⊥OP,PC交⊙O于C,
∴PC=PD,
∴利用相交弦定理可得AP×PB=PC×PD=PC2,
∵AP=4,PC=2,
∴PB=1.
故答案为:1
∵AB是⊙O的一条弦,点P为AB上一点,PC⊥OP,PC交⊙O于C,
∴PC=PD,
∴利用相交弦定理可得AP×PB=PC×PD=PC2,
∵AP=4,PC=2,
∴PB=1.
故答案为:1
点评:本题考查与圆有关的比例线段的应用,是基础题.解题时要认真审题,注意相交弦定理的合理运用.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
若曲线y=kx+lnx在点(1,k)处的切线平行x轴,则k=( )
| A、-1 | B、1 | C、-2 | D、2 |
已知函数f(x)=-x2+bx+c的图象的对称轴为直线x=2,则( )
| A、f(0)<f(1)<f(3) |
| B、f(3)<f(1)<f(0) |
| C、f(3)<f(1)=f(0) |
| D、f(0)<f(1)=f(3) |
双曲线x2-
=1上两点A、B关于直线y=-x+1对称,则直线AB方程为( )
| y2 |
| 3 |
| A、y=x | ||
| B、y=x+1 | ||
| C、y=x-1 | ||
D、y=x+
|
 如图,在四棱锥P-ABCD中,BC⊥平面PAB,且PA=PB=3,O是AB的中点,底面ABCD是直角梯形,AD∥BC,BC=1,AB=2,AD=3
如图,在四棱锥P-ABCD中,BC⊥平面PAB,且PA=PB=3,O是AB的中点,底面ABCD是直角梯形,AD∥BC,BC=1,AB=2,AD=3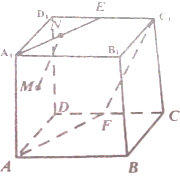 正方体AC1中,E,F分别是D1C1,DC的中点,N是A1E的中点,M为正方形A1ADD1的中心.
正方体AC1中,E,F分别是D1C1,DC的中点,N是A1E的中点,M为正方形A1ADD1的中心.