题目内容
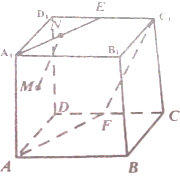 正方体AC1中,E,F分别是D1C1,DC的中点,N是A1E的中点,M为正方形A1ADD1的中心.
正方体AC1中,E,F分别是D1C1,DC的中点,N是A1E的中点,M为正方形A1ADD1的中心.(1)求证:∠ENM=∠C1FA
(2)求证:平面A1ME∥平面AFC1
(3)平面A1ME与平面AFC1将正方体分为3部分,求中间部分的体积.
考点:平面与平面平行的判定,棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:(1)连接A1D、DE,则所要证明的两角的边分别平行,利用等角定理证明.
(2)由第(1)问的线线平行关系,利用面面平行的判定定理可解决问题.
(3)先找出截正方体的两个截面,其中一个截面把正方体等分,另一个截面得三棱锥的体积可求,作差即可求出中间部分的体积.
(2)由第(1)问的线线平行关系,利用面面平行的判定定理可解决问题.
(3)先找出截正方体的两个截面,其中一个截面把正方体等分,另一个截面得三棱锥的体积可求,作差即可求出中间部分的体积.
解答:
解:(1)如图,连接A1D、DE

则MN为△A1DE的中位线,故MN∥DE,而DE∥FC1,
∴MN∥FC1,又∵AF∥A1E,
根据等角定理,∠ENM与∠C1FA相等或互补,又因为它们都是钝角,
∴∠ENM=∠C1FA
(2)由(1)知,MN∥FC1、AF∥A1E,
而MN、A1E是平面A1ME内的线,
由线面平行的判定定理知,FC1∥平面A1ME、AF∥平面A1ME,
∵FC1与AF是平面AFC1内的两条相交直线,根据面面平行的判定定理知,
平面A1ME∥平面AFC1
(3)取A1B1的中点G,连接C1G、AG,
则平面AFC1G为截面,它把正方体等分成两部分,
平面A1DE为平面A1ME截正方体的截面,
设正方体的棱长为a,则V三棱锥D-A1D1E=
×
a×
a×a=
a3,
∴V中间部分=
a3-V三棱锥D-A1D1E=
a3-
a3=
a3

则MN为△A1DE的中位线,故MN∥DE,而DE∥FC1,
∴MN∥FC1,又∵AF∥A1E,
根据等角定理,∠ENM与∠C1FA相等或互补,又因为它们都是钝角,
∴∠ENM=∠C1FA
(2)由(1)知,MN∥FC1、AF∥A1E,
而MN、A1E是平面A1ME内的线,
由线面平行的判定定理知,FC1∥平面A1ME、AF∥平面A1ME,
∵FC1与AF是平面AFC1内的两条相交直线,根据面面平行的判定定理知,
平面A1ME∥平面AFC1
(3)取A1B1的中点G,连接C1G、AG,
则平面AFC1G为截面,它把正方体等分成两部分,
平面A1DE为平面A1ME截正方体的截面,
设正方体的棱长为a,则V三棱锥D-A1D1E=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 12 |
∴V中间部分=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 12 |
| 5 |
| 12 |
点评:熟练掌握线面平行的判定和性质定理、正方体的性质、三角形的中位线定理、面面平行的判定定理、三棱锥的体积计算公式是解题的关键.

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
命题“存在x0∈R,2 x0≤0”的否定是( )
| A、不存在x0∈R,2 x0>0 |
| B、存在x0∈R,2 x0≥0 |
| C、对任意的x∈R,2x≤0 |
| D、对任意的x∈R,2x>0 |
 如图,点P为圆O的弦AB上的一点,连接PO,过点P作PC⊥OP,且PC交圆O于C.若AP=4,PC=2,则PB=
如图,点P为圆O的弦AB上的一点,连接PO,过点P作PC⊥OP,且PC交圆O于C.若AP=4,PC=2,则PB=