题目内容
1.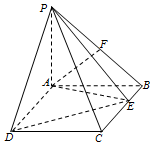 如图,PA⊥平面ABCD,四边形ABCD为矩形,PA=AB=2,AD=4,点F是PB的中点,点E在边BC上移动.
如图,PA⊥平面ABCD,四边形ABCD为矩形,PA=AB=2,AD=4,点F是PB的中点,点E在边BC上移动.(1)求三棱锥E-PAD的体积;
(2)证明:AF⊥PE.
分析 (1)由VE-PAD=VP-EAD,能求出三棱锥E-PAD的体积.
(2)法1:推导出PA⊥AB,AF⊥PB,从而BC⊥平面PAB,进而BC⊥AF,由AF⊥PB,AF⊥BC,得AF⊥平面PBC,由此能证明AF⊥PE.
法2:建立空间直角坐标系A-xyz,利用向量法能证明AF⊥PE.
解答 (本小题(12分),(1)小问(6分),(2)小问6分)
解:(1)∵PA⊥平面ABCD,四边形ABCD为矩形,
∴${S_{△EAD}}=\frac{1}{2}AD•AB=4$,
∴${V_{E-PAD}}={V_{P-EAD}}=\frac{1}{3}{S_{△EAD}}•PA=\frac{8}{3}$…(6分)
证明:(2)证法1:∵PA⊥平面ABCD,∴PA⊥AB,
又∵PA=AB=2,且点F是PB的中点,∴AF⊥PB,
又PA⊥BC,BC⊥AB,PA∩AB=A,
∴BC⊥平面PAB,…(9分)
又AF?平面PAB,∴BC⊥AF,
由AF⊥PB,AF⊥BC,PB∩BC=B,
∴AF⊥平面PBC,
∵PE?平面PBC,∴AF⊥PE…(12分)
证法2:如图建立空间直角坐标系A-xyz,
则A(0,0,0),P(0,0,2),B(0,2,0),C(4,2,0),…(8分)
∴F(0,1,1),∵点E在边BC上,设E(x,2,0)(0≤x≤4),
则 $\overrightarrow{AF}=(0\;,\;1\;,\;1)$,$\overrightarrow{PE}=(x\;,\;2\;,\;-2)$,…(10分)
∴$\overrightarrow{AF}•\overrightarrow{PE}=0$,∴AF⊥PE…(12分)
点评 本题考查线线垂直的证明,考查三棱锥的体积的求法,是中档题,考查推理论证能力、运算求解能力,考查转化化归思想、数形结合思想.

 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案| A. | y=$\frac{5}{3}$x | B. | y=$\frac{3}{5}$x | C. | y=±$\frac{5}{3}$x | D. | y=±$\frac{3}{5}$x |
| A. | [-3,3] | B. | [-9,3] | C. | $[-2-\sqrt{3}\;,\;2-\sqrt{3}]$ | D. | $[-3\sqrt{3}\;,\;3]$ |
(1)求不等式f(x)≤6的解集;
(2)若对任意$x∈[-\frac{1}{2},1]$,不等式f(x)≥|2x+a|-4恒成立,求实数a的取值范围.
| A. | $({\frac{1}{2},\frac{1}{4}})$ | B. | $({\frac{1}{4},\frac{1}{2}})$ | C. | $({\frac{{\sqrt{3}}}{4},0})$ | D. | $({0,\frac{{\sqrt{3}}}{4}})$ |
| A. | $\frac{1}{4}$ | B. | $\frac{7}{8}$ | C. | $\frac{1}{8}$ | D. | $\frac{7}{9}$ |
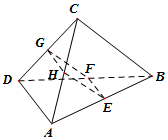 (文科)如图,在空间四面体ABCD中,若E,F,G,H分别是AB,BD,CD,AC的中点,
(文科)如图,在空间四面体ABCD中,若E,F,G,H分别是AB,BD,CD,AC的中点,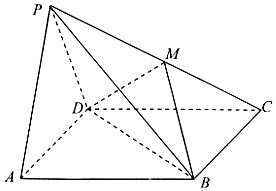 如图,四棱锥P-ABCD中,底面ABCD是矩形,平面PAD⊥底面ABCD,且△PAD是边长为2的等边三角形,PC=$\sqrt{13}$,M在PC上,且PA∥面MBD.
如图,四棱锥P-ABCD中,底面ABCD是矩形,平面PAD⊥底面ABCD,且△PAD是边长为2的等边三角形,PC=$\sqrt{13}$,M在PC上,且PA∥面MBD.