题目内容
已知点P1(a1,b1),P2(a2,b2),…Pn(an,bn)(n∈N+)都在函数y=log
x的图象上.
(Ⅰ)若数列{bn}是等差数列,求证:数列{an}是等比数列;
(2)若数列{bn}的前n项和为Sn,bn>0(n∈N+)且2Sn=bn2+bn,数列{cn}满足cn=2ancos2
π,求数列{cn}的前n项Tn.
| 1 |
| 2 |
(Ⅰ)若数列{bn}是等差数列,求证:数列{an}是等比数列;
(2)若数列{bn}的前n项和为Sn,bn>0(n∈N+)且2Sn=bn2+bn,数列{cn}满足cn=2ancos2
| π |
| 2 |
考点:数列的求和,等比数列的性质
专题:等差数列与等比数列
分析:(1)设公差为d,则bn+1-bn=d对∈N*恒成立,依题意an=(
)bn,数列{an}是等比数列.
(2)当n=1时,2S1=b12+b1,bn>0,b1=1.当n≥2,n∈N*时,2Sn-1=bn-12+bn-1,由此推导出bn=n.从而能求出数列{cn}的前n项Tn.
| 1 |
| 2 |
(2)当n=1时,2S1=b12+b1,bn>0,b1=1.当n≥2,n∈N*时,2Sn-1=bn-12+bn-1,由此推导出bn=n.从而能求出数列{cn}的前n项Tn.
解答:
(1)证明:∵数列{bn}是等差数列,
设公差为d,则bn+1-bn=d对∈N*恒成立,
依题意bn=log
an,∴an=(
)bn,
∴
=(
)bn+1-bn=(
)d是定值,
∴数列{an}是等比数列.
(2)解:当n=1时,2S1=b12+b1,bn>0,b1=1.
当n≥2,n∈N*时,2Sn-1=bn-12+bn-1,
∴2Sn-2Sn-1=bn2-bn-12+bn-bn-1,
bn+bn-1=(bn+bn-1)(bn-bn-1),
∵bn>0,∴bn-bn-1=1,n≥2,n∈N*,
∴数列{bn}是首项为1公差为1的等差数列,
∴bn=n.
由(1)知{an}是等比数列,且an=(
)n,
∵cn=2ancos2
π=an(cosnπ+1)=an(1)n+1=(-
)n+(
)n,
Tn=
+
(-
)n-(
)n.
设公差为d,则bn+1-bn=d对∈N*恒成立,
依题意bn=log
| 1 |
| 2 |
| 1 |
| 2 |
∴
| an+1 |
| an |
| 1 |
| 2 |
| 1 |
| 2 |
∴数列{an}是等比数列.
(2)解:当n=1时,2S1=b12+b1,bn>0,b1=1.
当n≥2,n∈N*时,2Sn-1=bn-12+bn-1,
∴2Sn-2Sn-1=bn2-bn-12+bn-bn-1,
bn+bn-1=(bn+bn-1)(bn-bn-1),
∵bn>0,∴bn-bn-1=1,n≥2,n∈N*,
∴数列{bn}是首项为1公差为1的等差数列,
∴bn=n.
由(1)知{an}是等比数列,且an=(
| 1 |
| 2 |
∵cn=2ancos2
| n |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
Tn=
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查等比数列的证明,考查数列的前n项和的求法,解题时要认真审题,注意构造法的合理运用.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案
相关题目
设Sn是等差数列{an}的前n项和,若
=
,则
( )
| S3 |
| S6 |
| 1 |
| 3 |
| S6 |
| S11 |
A、
| ||
B、
| ||
C、
| ||
D、
|
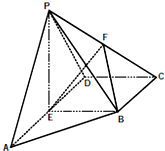 如图,在四棱锥P-ABCD中,E为AD的中点,F为PC的中点,PE⊥平面ABCD,AD∥BC,AD⊥CD,且BC=CD=
如图,在四棱锥P-ABCD中,E为AD的中点,F为PC的中点,PE⊥平面ABCD,AD∥BC,AD⊥CD,且BC=CD=