题目内容
已知f(x)=4ax-m•2x+1.
(1)当a=1时,函数f(x)在[0,log23]上的最小值为-4,求实数m的值;
(2)当m=1时,若f(x)≥2x在[1,2]上恒成立,求实数a的取值范围.
(1)当a=1时,函数f(x)在[0,log23]上的最小值为-4,求实数m的值;
(2)当m=1时,若f(x)≥2x在[1,2]上恒成立,求实数a的取值范围.
考点:函数恒成立问题,复合函数的单调性
专题:函数的性质及应用
分析:(1)当a=1时,函数f(x)=4x-2m2x,利用换元法结合一元二次函数的性质即可求出m的值;
(2)当m=1时,f(x)≥2x?4ax-2x+1≥2x,两边取对数,log24ax≥log23•2x,得出2ax≥x+log23,进一步整理得2a≥
+1,
求最值,使2a≥(
+1)最小值即可求出a的范围.
(2)当m=1时,f(x)≥2x?4ax-2x+1≥2x,两边取对数,log24ax≥log23•2x,得出2ax≥x+log23,进一步整理得2a≥
| log23 |
| x |
求最值,使2a≥(
| log23 |
| x |
解答:
解:(1)当a=1时,函数f(x)=4x-2m2x,
f(x)=(2x)2-2m•2x,
令t=2x,则t∈[1,3],
则函数等价为y=g(t)=t2-2mt=(t-m)2-m2,
①m≥3时,f(x)min=g(3)=9-6m=-4,∴m=
(舍);
②1<m<3时,f(x)min=g(m)=-m2=-4,∴m=2;
③m≤1时,f(x)min=g(1)=1-2m=-4,∴m=
(舍);
综上,m=2
(2)当m=1时,f(x)≥2x?4ax-2x+1≥2x,
∴4ax≥3•2x,两边取对数,log24ax≥log23•2x,∴2ax≥x+log23
∴2a≥
+1,x∈[1,2]恒成立,
当x=1时,(
+1)最小值=1+log23,
∴2a≥1+log23,
∴a≥
.
f(x)=(2x)2-2m•2x,
令t=2x,则t∈[1,3],
则函数等价为y=g(t)=t2-2mt=(t-m)2-m2,
①m≥3时,f(x)min=g(3)=9-6m=-4,∴m=
| 13 |
| 6 |
②1<m<3时,f(x)min=g(m)=-m2=-4,∴m=2;
③m≤1时,f(x)min=g(1)=1-2m=-4,∴m=
| 5 |
| 2 |
综上,m=2
(2)当m=1时,f(x)≥2x?4ax-2x+1≥2x,
∴4ax≥3•2x,两边取对数,log24ax≥log23•2x,∴2ax≥x+log23
∴2a≥
| log23 |
| x |
当x=1时,(
| log23 |
| x |
∴2a≥1+log23,
∴a≥
| 1+log23 |
| 2 |
点评:本题主要考查与指数函数有关的性质是运算,同时考查函数恒成立的问题,利用换元法结合一元二次函数的性质是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如图Rt△O′A′B′是一平面图形的直观图,直角边O′B′=2,则这个平面图形的面积是( )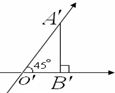

A、2
| ||
| B、1 | ||
C、4
| ||
D、
|
已知点A(n,m)和点B(n+1,t)在二次函数y=x2的图象上,n为正整数,直线AB与x轴所成的锐角的大小为α,则tanα=( )
| A、n+1 | B、2n+1 |
| C、n-1 | D、2n-1 |
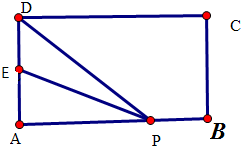 如图,在矩形ABCD中,E是AD的中点,P是AB边上的点,AB=3,AD=2
如图,在矩形ABCD中,E是AD的中点,P是AB边上的点,AB=3,AD=2