题目内容
已知点A(n,m)和点B(n+1,t)在二次函数y=x2的图象上,n为正整数,直线AB与x轴所成的锐角的大小为α,则tanα=( )
| A、n+1 | B、2n+1 |
| C、n-1 | D、2n-1 |
考点:二次函数的性质
专题:函数的性质及应用
分析:根的函数解析式得出A(n,n2)和点B(n+1,(n+1)2),运用斜率公式得出kAB=
=2n+1,即可求出tanα.
| (n+1)2-n2 |
| (n+1)-n |
解答:
解:∵点A(n,m)和点B(n+1,t)在二次函数y=x2的图象上,n为正整数,
∴A(n,n2)和点B(n+1,(n+1)2),
∴kAB=
=2n+1,
∴则tanα=2n+1,
故选:B.
∴A(n,n2)和点B(n+1,(n+1)2),
∴kAB=
| (n+1)2-n2 |
| (n+1)-n |
∴则tanα=2n+1,
故选:B.
点评:本题考查了二次函数的性质,直线的斜率的概念,公式,属于容易题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知命题p:“?x∈[1,2],x2-a≥0”,命题q:“?x∈R,x2+2ax+2-a=0”.若命题“p且q”是真命题,则实数a的取值范围为( )
| A、-2≤a≤1 |
| B、a≤-2或1≤a≤2 |
| C、a≥1 |
| D、a≤-2或 a=1 |
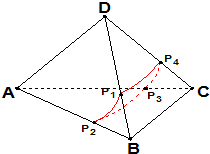 如图,四面体ABCD中,DA=DB=DC=1,且DA、DB、DC两两互相垂直,在该四面体表面上与点A距离是
如图,四面体ABCD中,DA=DB=DC=1,且DA、DB、DC两两互相垂直,在该四面体表面上与点A距离是