题目内容
数列{an}为正项等比数列,它的前k项和为80,其中最大项为54,前2k项和为6560,其中k∈N*
(Ⅰ)求数列{an}的首项a1和公比q;
(Ⅱ)设bn=log2an,n∈N*,求数列{bn}的前n项和b1+b2+b3+…+bn.
(Ⅰ)求数列{an}的首项a1和公比q;
(Ⅱ)设bn=log2an,n∈N*,求数列{bn}的前n项和b1+b2+b3+…+bn.
考点:数列的求和,等比数列的性质
专题:等差数列与等比数列
分析:(Ⅰ)根据S2n-Sn=6480>Sn,可推断出公比大于1,即数列为递增数列,故可知第n项为数值的最大项.与Sn=80,S2n=6560联立方程可求得首项a和q的值.
(Ⅱ)由由(Ⅰ)可知an=2×3n-1,继而得到b1+b2+b3+…+bn=n+(0+1+2+…+n-1)log23,求的结果即可.
(Ⅱ)由由(Ⅰ)可知an=2×3n-1,继而得到b1+b2+b3+…+bn=n+(0+1+2+…+n-1)log23,求的结果即可.
解答:
解:(Ⅰ)设公比为q,∵S2n-Sn=6480>Sn,
∴q>1.
又由an>0,则最大项是an=a1qn-1=54;①
又Sn=
=80,②
S2n=
=6560,③
由①②③解得a1=2,q=3.
(Ⅱ)由(Ⅰ)可知an=2×3n-1,
∴bn=log22×3n-1=1+(n-1)log23,
∴b1+b2+b3+…+bn=n+(0+1+2+…+n-1)log23=n+
log23.
∴q>1.
又由an>0,则最大项是an=a1qn-1=54;①
又Sn=
| a1(1-qn) |
| 1-q |
S2n=
| a1(1-q2n) |
| 1-q |
由①②③解得a1=2,q=3.
(Ⅱ)由(Ⅰ)可知an=2×3n-1,
∴bn=log22×3n-1=1+(n-1)log23,
∴b1+b2+b3+…+bn=n+(0+1+2+…+n-1)log23=n+
| n(n-1) |
| 2 |
点评:本题考查了等比数列的通项公式,以及求和公式,解题的关键是通过判断数列的递增或递减找到数值最大项.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知一个算法的流程图如图所示,则输出的结果是( )


| A、2 | B、5 | C、25 | D、26 |
设
,
,
为单位向量,
,
的夹角为60°,则(
+
)•
的最大值为( )
| a |
| b |
| c |
| a |
| b |
| a |
| b |
| c |
A、
| ||
B、
| ||
| C、3 | ||
| D、2 |
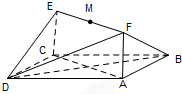 如图所示,已知矩形ABCD和矩形ACEF所在的平面互相垂直,AB=
如图所示,已知矩形ABCD和矩形ACEF所在的平面互相垂直,AB=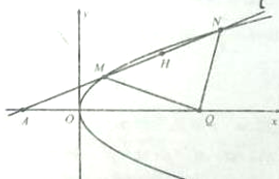 已知抛物线y2=4x,直线l:y=kx+2(k>0)与抛物线C交于M、N两点,与x轴交于点A,H 为MN的中点,O为坐标原点.
已知抛物线y2=4x,直线l:y=kx+2(k>0)与抛物线C交于M、N两点,与x轴交于点A,H 为MN的中点,O为坐标原点.